
The idea of a quotient group follows easily from cosets and Lagrange's theorem. In this video, we start with a normal subgroup and develop the idea of a quotient group, by viewing each coset (together with the normal subgroup) as individual mathematical objects in a set. This set, under
From playlist Abstract algebra

Now that we know what a quotient group is, let's take a look at an example to cement our understanding of the concepts involved.
From playlist Abstract algebra

RNT1.4. Ideals and Quotient Rings
Ring Theory: We define ideals in rings as an analogue of normal subgroups in group theory. We give a correspondence between (two-sided) ideals and kernels of homomorphisms using quotient rings. We also state the First Isomorphism Theorem for Rings and give examples.
From playlist Abstract Algebra

Abstract Algebra | The motivation for the definition of an ideal.
Towards the goal of creating a quotient ring, we uncover the defintion of an ideal. http://www.michael-penn.net https://www.researchgate.net/profile/Michael_Penn5 http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Chapter 5: Quotient groups | Essence of Group Theory
Quotient groups is a very important concept in group theory, because it has paramount importance in group homomorphisms (connection with the isomorphism theorem(s)). With this video series, abstract algebra needs not be abstract - one can easily develop intuitions for group theory! In fac
From playlist Essence of Group Theory

Fundamentals of Mathematics - Lecture 25: Quotient Maps (Real Projective Line, Modular Arithmetic)
course page - https://www.uvm.edu/~tdupuy/logic/Math52-Fall2017.html videography - Eric Melton, UVM
From playlist Fundamentals of Mathematics

Abstract Algebra | Quotient Groups
We introduce the notion of a quotient group and give some examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Learn the basics for simplifying an expression using the rules of exponents
👉 Learn how to simplify expressions using the quotient rule of exponents. The quotient rule of exponents states that the quotient of powers with a common base is equivalent to the power with the common base and an exponent which is the difference of the exponents of the term in the numerat
From playlist Simplify Using the Rules of Exponents | Quotient Rule

Algebra - Quotient rule for exponents
This video show how to use the quotient rule for exponents. Remember that when using the quotient rule we can subtract the exponents. For more videos visit http://www.mysecretmathtutor.com
From playlist Algebra

Moduli of Representations and Pseudorepresentations - Carl Wang Erickson
Carl Wang Erickson Harvard University May 2, 2013 A continuous representation of a profinite group induces a continuous pseudorepresentation, where a pseudorepresentation is the data of the characteristic polynomial coefficients. We discuss the geometry of the resulting map from the moduli
From playlist Mathematics

Benjamin Anderson-Sackaney - Tracial and G-invariant States on Quantum Groups
For a discrete group G, the tracial states on its reduced group $C^*$-algebra $C^∗_r (G)$ are exactly the conjugation invariant states. This makes the traces on $C^∗_r (G)$ amenable to group dynamical techniques. In the setting of a discrete quantum group ${\mathbb G}$, there is a quantum
From playlist Annual meeting “Arbre de Noël du GDR Géométrie non-commutative”

Emily Cliff: Hilbert Schemes Lecture 3
SMRI Seminar Series: 'Hilbert Schemes' Lecture 3 The universal family on H Emily Cliff (University of Sydney) This series of lectures aims to present parts of Nakajima’s book `Lectures on Hilbert schemes of points on surfaces’ in a way that is accessible to PhD students interested in rep
From playlist SMRI Course: Hilbert Schemes

Holomorphic Curves in Compact Quotients of SL(2,C) by Sorin Dumitrescu
DISCUSSION MEETING TOPICS IN HODGE THEORY (HYBRID) ORGANIZERS: Indranil Biswas (TIFR, Mumbai, India) and Mahan Mj (TIFR, Mumbai, India) DATE: 20 February 2023 to 25 February 2023 VENUE: Ramanujan Lecture Hall and Online This is a followup discussion meeting on complex and algebraic ge
From playlist Topics in Hodge Theory - 2023

Approximations of groups, subquotients of infinite direct products and equations... - Lev Glebsky
Stability and Testability Topic: Approximations of groups, subquotients of infinite direct products and equations over groups Speaker: Lev Glebsky Affiliation: Universidad Autónoma de San Luis Potosí Date: November 25 2020 For more video please visit http://video.ias.edu Glebsky-2020-11-
From playlist Stability and Testability

Permutation Orbifolds of Vertex Operator Algebras
This is a recording of a talk I gave at the Illinois State University Algebra Seminar. Suggest a problem: https://forms.gle/ea7Pw7HcKePGB4my5 Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Merch: https://teespring.com/stores/michael-penn-math Personal Websi
From playlist Research Talks

Sergio Zamora (1/20/23): The lower semi-continuity of \pi_1 and nilpotent structures in persistence
When a sequence of compact geodesic spaces X_i converges to a compact geodesic space X, under minimal assumptions there are surjective morphisms $\pi_1(X_i) \to \pi_1(X)$ for i large enough. In particular, a limit of simply connected spaces is simply connected. This is clearly not true for
From playlist Vietoris-Rips Seminar

Felix Klein Lectures 2020: Quiver moduli and applications, Markus Reineke (Bochum), Lecture 2
Quiver moduli spaces are algebraic varieties encoding the continuous parameters of linear algebra type classification problems. In recent years their topological and geometric properties have been explored, and applications to, among others, Donaldson-Thomas and Gromov-Witten theory have
From playlist Felix Klein Lectures 2020: Quiver moduli and applications, Markus Reineke (Bochum)

A Hecke action on the principal block of a semisimple algebraic group - Simon Riche
Workshop on Representation Theory and Geometry Topic: A Hecke action on the principal block of a semisimple algebraic group Speaker: Simon Riche Affiliation: Université Paris 6; Member, School of Mathematics Date: April 01, 2021 For more video please visit http://video.ias.edu
From playlist Mathematics
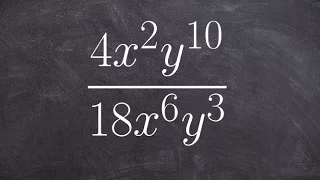
Simplify an expression by applying quotient rule of exponents
👉 Learn how to simplify expressions using the quotient rule of exponents. The quotient rule of exponents states that the quotient of powers with a common base is equivalent to the power with the common base and an exponent which is the difference of the exponents of the term in the numerat
From playlist Simplify Using the Rules of Exponents | Quotient Rule

Gromov-Witten Theory and Gauge Theory (Lecture 2) by Constantin Teleman
PROGRAM: VORTEX MODULI ORGANIZERS: Nuno Romão (University of Augsburg, Germany) and Sushmita Venugopalan (IMSc, India) DATE & TIME: 06 February 2023 to 17 February 2023 VENUE: Ramanujan Lecture Hall, ICTS Bengaluru For a long time, the vortex equations and their associated self-dual fie
From playlist Vortex Moduli - 2023