
Vector form of multivariable quadratic approximation
This is the more general form of a quadratic approximation for a scalar-valued multivariable function. It is analogous to a quadratic Taylor polynomial in the single-variable world.
From playlist Multivariable calculus

Summary for solving using the difference of two squares
👉Learn how to solve quadratic functions. Quadratic equations are equations whose highest power in the variable(s) is 2. They are of the form y = ax^2 + bx + c. There are various techniques which can be applied in solving quadratic equations. Some of the techniques includes factoring and th
From playlist Solve Quadratic Equations by Factoring

Summary for solving a quadratic
👉Learn how to solve quadratic functions. Quadratic equations are equations whose highest power in the variable(s) is 2. They are of the form y = ax^2 + bx + c. There are various techniques which can be applied in solving quadratic equations. Some of the techniques includes factoring and th
From playlist Solve Quadratic Equations by Factoring

What does solving a quadratic mean
👉Learn how to solve quadratic functions. Quadratic equations are equations whose highest power in the variable(s) is 2. They are of the form y = ax^2 + bx + c. There are various techniques which can be applied in solving quadratic equations. Some of the techniques includes factoring and th
From playlist Solve Quadratic Equations by Factoring

What are perfect squares and how do we use them
👉Learn how to solve quadratic functions. Quadratic equations are equations whose highest power in the variable(s) is 2. They are of the form y = ax^2 + bx + c. There are various techniques which can be applied in solving quadratic equations. Some of the techniques includes factoring and th
From playlist Solve Quadratic Equations by Factoring
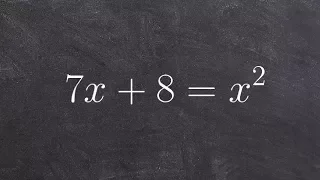
How to factor and solve a trinomial when it is not set to zero
👉Learn how to solve quadratic equations by factoring when a is equal to 1. A quadratic is an algebraic expression having 2 as the highest power of its variable(s). To factor an algebraic expression means to break it up into factors (expressions that can be multiplied together to get the or
From playlist Solve Quadratic Equations by Factoring

Walter CRAIG - Birkhoff normal form for nonlinear wave equations
Many theorems on global existence of small amplitude solutions of nonlinear wave equations in ${\mathbb R}^n$ depend upon a competition between the time decay of solutions and the degree of the nonlinearity. Decay estimates are more effective when inessential nonlinea
From playlist Trimestre "Ondes Non Linéaires" - May Conference

Jayce Getz: New avenues for the circle method, Lecture III
Motivated by research arising from automorphic representation theory, I will present someideas that should open up new avenues of research in the circle method. In the first half of the lecturesI will discuss an adelic version of the delta-method of Duke, Friedlander, Iwaniec and Heath-Br
From playlist Hausdorff School "The Circle Method"

Jayce Getz: New avenues for the circle method, Lecture IV
Motivated by research arising from automorphic representation theory, I will present some ideas that should open up new avenues of research in the circle method. In the first half of the lectures I will discuss an adelic version of the delta-method of Duke, Friedlander, Iwaniec and Heath-B
From playlist Hausdorff School "The Circle Method"

On triple product L functions - Jayce Robert Getz
Joint IAS/Princeton University Number Theory Seminar Topic: On triple product L functions Speaker: Jayce Robert Getz Affiliation: Duke University Date: May 7, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

Lynne Walling: Understanding quadratic forms on lattices through generalised theta series
Abstract: Siegel introduced generalised theta series to study representation numbers of quadratic forms. Given an integral lattice L with quadratic form q, Siegel’s degree n theta series attached to L has a Fourier expansion supported on n-dimensional lattices, with Fourier coefficients th
From playlist Women at CIRM

Suhasini Subba Rao: Reconciling the Gaussian and Whittle Likelihood with an application to ...
In time series analysis there is an apparent dichotomy between time and frequency domain methods. The aim of this paper is to draw connections between frequency and time domain methods. Our focus will be on reconciling the Gaussia likelihood and the Whittle likelihood. We derive an exact,
From playlist Virtual Conference

Determine the roots of the quadratic function with fraction coefficients
👉Learn how to solve quadratic equations by factoring when a is equal to 1. A quadratic is an algebraic expression having 2 as the highest power of its variable(s). To factor an algebraic expression means to break it up into factors (expressions that can be multiplied together to get the or
From playlist Solve Quadratic Equations by Factoring

Summary for solving a quadratic by factoring using various methods
👉Learn how to solve quadratic functions. Quadratic equations are equations whose highest power in the variable(s) is 2. They are of the form y = ax^2 + bx + c. There are various techniques which can be applied in solving quadratic equations. Some of the techniques includes factoring and th
From playlist Solve Quadratic Equations by Factoring

Summation formulae and speculations on period integrals attached to triples... - Jayce Getz
Joint IAS/Princeton University Number Theory Seminar Topic: Summation formulae and speculations on period integrals attached to triples of automorphic representations Speaker: Jayce Getz Affiliation: Date: March 27, 2018 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Solving a quadratic by factoring a trinomial when a is equal to one
👉Learn how to solve quadratic equations by factoring when a is equal to 1. A quadratic is an algebraic expression having 2 as the highest power of its variable(s). To factor an algebraic expression means to break it up into factors (expressions that can be multiplied together to get the or
From playlist Solve Quadratic Equations by Factoring

1. Collective Behavior, from Particles to Fields Part 1
MIT 8.334 Statistical Mechanics II: Statistical Physics of Fields, Spring 2014 View the complete course: http://ocw.mit.edu/8-334S14 Instructor: Mehran Kardar In this lecture, Prof. Kardar introduces the principles of collective behavior from particles to fields, including Phonons and Ela
From playlist MIT 8.334 Statistical Mechanics II, Spring 2014

Jayce Getz: New avenues for the circle method, Lecture II
Motivated by research arising from automorphic representation theory, I will present someideas that should open up new avenues of research in the circle method. In the first half of the lecturesI will discuss an adelic version of the delta-method of Duke, Friedlander, Iwaniec and Heath-Br
From playlist Hausdorff School "The Circle Method"

Global Existence of Surface Waves - Jalal Shatah
Jalal Shatah Courant Institute, NYU March 2, 2012 For more videos, visit http://video.ias.edu
From playlist Mathematics

What do i need to know to solve using the difference of two squares
👉Learn how to solve quadratic functions. Quadratic equations are equations whose highest power in the variable(s) is 2. They are of the form y = ax^2 + bx + c. There are various techniques which can be applied in solving quadratic equations. Some of the techniques includes factoring and th
From playlist Solve Quadratic Equations by Factoring