
Serguei Ivachkovitch - Method of pseudoholomorphic curves and applications (Part 4)
The method of « pseudoholomorphic » curves proved itself to be extremely useful in different fields. In symplectic topology, for instance Gromov’s Nonsqueezing Theorem, Arnold’s conjecture and the Floer homology, the Gromov-Witten invariants. In complex analysis and geometry, for instane p
From playlist École d’été 2012 - Feuilletages, Courbes pseudoholomorphes, Applications

Serguei Ivachkovitch - Method of pseudoholomorphic curves and applications (Part 3)
The method of « pseudoholomorphic » curves proved itself to be extremely useful in different fields. In symplectic topology, for instance Gromov’s Nonsqueezing Theorem, Arnold’s conjecture and the Floer homology, the Gromov-Witten invariants. In complex analysis and geometry, for instane p
From playlist École d’été 2012 - Feuilletages, Courbes pseudoholomorphes, Applications
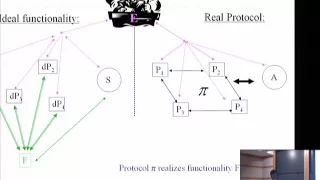
A Completeness Theorem for Pseudo-Linear Functions with App... - Charanjit Jutla
Charanjit Jutla IBM T. J. Watson Research Center February 28, 2010 We prove completeness results for certain class of functions which have implications for automatic proving of universally-composable security theorems for ideal and real functionalities composed of if-then-else programs wi
From playlist Mathematics

Serguei Ivachkovitch - Method of pseudoholomorphic curves and applications (Part 1)
The method of « pseudoholomorphic » curves proved itself to be extremely useful in different fields. In symplectic topology, for instance Gromov’s Nonsqueezing Theorem, Arnold’s conjecture and the Floer homology, the Gromov-Witten invariants. In complex analysis and geometry, for instane p
From playlist École d’été 2012 - Feuilletages, Courbes pseudoholomorphes, Applications

Weil conjectures 1 Introduction
This talk is the first of a series of talks on the Weil conejctures. We recall properties of the Riemann zeta function, and describe how Artin used these to motivate the definition of the zeta function of a curve over a finite field. We then describe Weil's generalization of this to varie
From playlist Algebraic geometry: extra topics
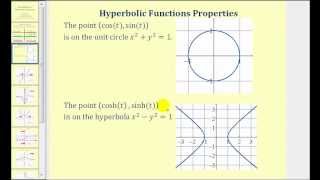
Introduction to Hyperbolic Functions
This video provides a basic overview of hyperbolic function. The lesson defines the hyperbolic functions, shows the graphs of the hyperbolic functions, and gives the properties of hyperbolic functions. Site: http://mathispower4u.com Blog: http://mathispower4u.wordpress.com
From playlist Differentiation of Hyperbolic Functions
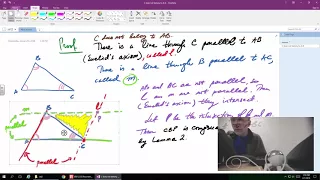
A theorem about isosceles -- Proofs
This lecture is on Introduction to Higher Mathematics (Proofs). For more see http://calculus123.com.
From playlist Proofs

Jean-Pierre Demailly - Kobayashi pseudo-metrics, entire curves and hyperbolicity of ... (Part 1)
We will first introduce the basic concepts pertaining to Kobayashi pseudo-distances and hyperbolic complex spaces, including Brody’s theorem and the Ahlfors-Schwarz lemma. One of the main goals of the theory is to understand conditions under which a given algebraic variety is Kobayashi hyp
From playlist École d’été 2012 - Feuilletages, Courbes pseudoholomorphes, Applications

Jean-Pierre Demailly - Kobayashi pseudo-metrics, entire curves and hyperbolicity of ... (Part 3)
We will first introduce the basic concepts pertaining to Kobayashi pseudo-distances and hyperbolic complex spaces, including Brody’s theorem and the Ahlfors-Schwarz lemma. One of the main goals of the theory is to understand conditions under which a given algebraic variety is Kobayashi hyp
From playlist École d’été 2012 - Feuilletages, Courbes pseudoholomorphes, Applications

Calculus 1 (Stewart) Ep 22, Mean Value Theorem (Oct 28, 2021)
This is a recording of a live class for Math 1171, Calculus 1, an undergraduate course for math majors (and others) at Fairfield University, Fall 2021. The textbook is Stewart. PDF of the written notes, and a list of all episodes is at the class website. Class website: http://cstaecker.f
From playlist Math 1171 (Calculus 1) Fall 2021

Equidistribution of Unipotent Random Walks on Homogeneous spaces by Emmanuel Breuillard
PROGRAM : ERGODIC THEORY AND DYNAMICAL SYSTEMS (HYBRID) ORGANIZERS : C. S. Aravinda (TIFR-CAM, Bengaluru), Anish Ghosh (TIFR, Mumbai) and Riddhi Shah (JNU, New Delhi) DATE : 05 December 2022 to 16 December 2022 VENUE : Ramanujan Lecture Hall and Online The programme will have an emphasis
From playlist Ergodic Theory and Dynamical Systems 2022

What is Green's theorem? Chris Tisdell UNSW
This lecture discusses Green's theorem in the plane. Green's theorem not only gives a relationship between double integrals and line integrals, but it also gives a relationship between "curl" and "circulation". In addition, Gauss' divergence theorem in the plane is also discussed, whic
From playlist Vector Calculus @ UNSW Sydney. Dr Chris Tisdell

Real Analysis Ep 32: The Mean Value Theorem
Episode 32 of my videos for my undergraduate Real Analysis course at Fairfield University. This is a recording of a live class. This episode is more about the mean value theorem and related ideas. Class webpage: http://cstaecker.fairfield.edu/~cstaecker/courses/2020f3371/ Chris Staecker
From playlist Math 3371 (Real analysis) Fall 2020

Pythagorean theorem - What is it?
► My Geometry course: https://www.kristakingmath.com/geometry-course Pythagorean theorem is super important in math. You will probably learn about it for the first time in Algebra, but you will literally use it in Algebra, Geometry, Trigonometry, Precalculus, Calculus, and beyond! That’s
From playlist Geometry

Wolfram Physics Project: Working Session Sept. 15, 2020 [Physicalization of Metamathematics]
This is a Wolfram Physics Project working session on metamathematics and its physicalization in the Wolfram Model. Begins at 10:15 Originally livestreamed at: https://twitch.tv/stephen_wolfram Stay up-to-date on this project by visiting our website: http://wolfr.am/physics Check out the
From playlist Wolfram Physics Project Livestream Archive

Johnathan Bush (7/8/2020): Borsuk–Ulam theorems for maps into higher-dimensional codomains
Title: Borsuk–Ulam theorems for maps into higher-dimensional codomains Abstract: I will describe Borsuk-Ulam theorems for maps of spheres into higher-dimensional codomains. Given a continuous map from a sphere to Euclidean space, we say the map is odd if it respects the standard antipodal
From playlist AATRN 2020

Worldwide Calculus: Extrema and the Mean Value Theorem
Lecture on 'Extrema and the Mean Value Theorem' from 'Worldwide Differential Calculus' and 'Worldwide AP Calculus'. For more lecture videos and $10 digital textbooks, visit www.centerofmath.org.
From playlist Worldwide Single-Variable Calculus for AP®

Stokes' Theorem and Green's Theorem
Stokes' theorem is an extremely powerful result in mathematical physics. It allows us to quantify how much a vector field is circulating or rotating, based on the integral of the curl. @eigensteve on Twitter eigensteve.com databookuw.com %%% CHAPTERS %%% 0:00 Stoke's Theorem Overview
From playlist Engineering Math: Vector Calculus and Partial Differential Equations

Green's Theorem. Chris Tisdell UNSW
This is the 2nd lecture on Green's theorem and its use. In this lecture we explore some interesting applications of Green's theorem and present several examples. Also some proofs are discussed.
From playlist Vector Calculus @ UNSW Sydney. Dr Chris Tisdell

Jean-Pierre Demailly - Kobayashi pseudo-metrics, entire curves and hyperbolicity of ... (Part 4)
We will first introduce the basic concepts pertaining to Kobayashi pseudo-distances and hyperbolic complex spaces, including Brody’s theorem and the Ahlfors-Schwarz lemma. One of the main goals of the theory is to understand conditions under which a given algebraic variety is Kobayashi hyp
From playlist École d’été 2012 - Feuilletages, Courbes pseudoholomorphes, Applications