
What are four types of polygons
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

What are the names of different types of polygons based on the number of sides
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

What is the difference between convex and concave polygons
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

What is the definition of a regular polygon and how do you find the interior angles
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

What is the difference between convex and concave
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

What is a polygon and what is a non example of a one
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons
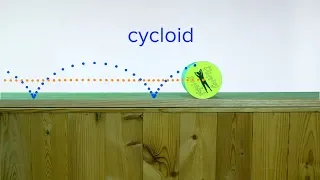
#Cycloid: A curve traced by a point on a circle rolling in a straight line. (A preview of this Sunday's video.)
From playlist Miscellaneous