Projective frame

Projective geometry

In mathematics, and more specifically in projective geometry, a projective frame or projective basis is a tuple of points in a projective space that can be used for defining homogeneous coordinates in this space. More precisely, in a projective space of dimension n, a projective frame is a n + 2-tuple of points such that no hyperplane contains n + 1 of them. A projective frame is sometimes called a simplex, although a simplex in a space of dimension n has at most n + 1 vertices. In this article, only projective spaces over a field K are considered, although most results can be generalized to projective spaces over a division ring. Let P(V) be a projective space of dimension n, where V is a K-vector space of dimension n + 1. Let be the canonical projection that maps a nonzero vector v to the corresponding point of P(V), which is the vector line that contains v. Every frame of P(V) can be written as for some vectors of V. The definition implies the existence of nonzero elements of K such that . Replacing by for and by , one gets the following characterization of a frame: n + 2 points of P(V) form a frame if and only if they are the image by p of a basis of V and the sum of its elements. Moreover, two bases define the same frame in this way, if and only if the elements of the second one are the products of the elements of the first one by a fixed nonzero element of K. As homographies of P(V) are induced by linear endomorphisms of V, it follows that, given two frames, there is exactly one homography mapping the first one onto the second one. In particular, the only homography fixing the points of a frame is the identity map. This result is much more difficult in synthetic geometry (where projective spaces are defined through axioms). It is sometimes called the first fundamental theorem of projective geometry. Every frame can be written as where is basis of V. The projective coordinates or homogeneous coordinates of a point p(v) over this frame are the coordinates of the vector v on the basis If one changes the vectors representing the point p(v) and the frame elements, the coordinates are multiplied by a fixed nonzero scalar. Commonly, the projective space Pn(K) = P(Kn+1) is considered. It has a canonical frame consisting of the image by p of the canonical basis of Kn+1 (consisting of the elements having only one nonzero entry, which is equal to 1), and (1, 1, ..., 1). On this basis, the homogeneous coordinates of p(v) are simply the entries (coefficients) of v. Given another projective space P(V) of the same dimension n, and a frame F of it, there is exactly one homography h mapping F onto the canonical frame of P(Kn+1). The projective coordinates of a point a on the frame F are the homogeneous coordinates of h(a) on the canonical frame of Pn(K). In the case of a projective line, a frame consists of three distinct points. If P1(K) is identified with K with a point at infinity ∞ added, then its canonical frame is (∞, 0, 1). Given any frame (a0, a1, a2), the projective coordinates of a point a ≠ a0 are (r, 1), where r is the cross-ratio (a, a2; a1, a0). If a = a0, the cross ratio is the infinity, and the projective coordinates are (1,0). (Wikipedia).

Introduction to Projective Geometry (Part 1)

The first video in a series on projective geometry. We discuss the motivation for studying projective planes, and list the axioms of affine planes.

From playlist Introduction to Projective Geometry

The circle and projective homogeneous coordinates | Universal Hyperbolic Geometry 7a | NJ Wildberger

Universal hyperbolic geometry is based on projective geometry. This video introduces this important subject, which these days is sadly absent from most undergrad/college curriculums. We adopt the 19th century view of a projective space as the space of one-dimensional subspaces of an affine

From playlist Universal Hyperbolic Geometry

The circle and projective homogeneous coordinates (cont.) | Universal Hyperbolic Geometry 7b

From playlist Universal Hyperbolic Geometry

algebraic geometry 15 Projective space

This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It introduces projective space and describes the synthetic and analytic approaches to projective geometry

From playlist Algebraic geometry I: Varieties

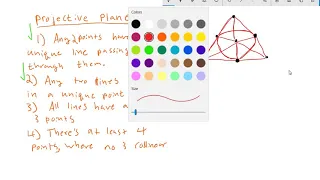
Introduction to Projective Geometry (Part 2)

The second video in a series about projective geometry. We list the axioms for projective planes, give an examle of a projective plane with finitely many points, and define the real projective plane.

From playlist Introduction to Projective Geometry

Algebraic structure on the Euclidean projective line | Rational Geometry Math Foundations 137

In this video we look at some pleasant consequences of imposing a Euclidean structure on the projective line. We give a proof of the fundamental projective Triple quad formula, talk about the equal p-quadrances theorem, and see how the logistic map of chaos theory makes its appearance as t

From playlist Math Foundations

Projective view of conics and quadrics | Differential Geometry 9 | NJ Wildberger

In this video we introduce projective geometry into the study of conics and quadrics. Our point of view follows Mobius and Plucker: the projective plane is considered as the space of one-dimensional subspaces of a three dimensional vector space, or in other words lines through the origin.

From playlist Differential Geometry

Reference Frames (9.1)

In this video, I define "inertial reference frame," "non-inertial reference frame," and "inertial force."

From playlist Intermediate Classical Mechanics

The projective Quadruple quad formula | Rational Geometry Math Foundations 148 | NJ Wildberger

In this video we introduce the projective version of the Quadruple quad formula, which not only controls the relationship between four projective points, but has a surprising connection with the geometry of the cyclic quadrilateral. The projective quadruple quad function is called R(a,b,

From playlist Math Foundations

Live CEOing Ep 645: Language Design Review of Astronomy, Geography & More Continued

In this episode of Live CEOing, Stephen Wolfram discusses upcoming improvements and features to the Wolfram Language. If you'd like to contribute to the discussion in future episodes, you can participate through this YouTube channel or through the official Twitch channel of Stephen Wolfram

From playlist Behind the Scenes in Real-Life Software Design

Highlight: Adding iframes to the streamer so they can last longer

Brooks changed the way that iframes work in the Get the Streamer game! Now the streamer gets more iframes at the beginning of the game and the number of them goes down the longer the game goes on. This way the streamer has a better chance at lasting longer into the game. --- Code - [http

From playlist programming before work live streams

Seminar on Applied Geometry and Algebra (SIAM SAGA): Dustin Mixon

Title: Packing Points in Projective Spaces Speaker: Dustin Mixon Date: Tuesday, March 8, 2022 at 11:00am Eastern Abstract: Given a compact metric space, it is natural to ask how to arrange a given number of points so that the minimum distance is maximized. For example, the setting of the

From playlist Seminar on Applied Geometry and Algebra (SIAM SAGA)

Using a Homogeneous Transformation Matrix to Combine Rotation and Translation

In this video we discuss how to properly deal with coordinate frames that are both rotated and translated from one another. We develop a homogeneous transformation matrix which combines a standard rotation matrix with a translation. This matrix can be used to relate the pose of a system

From playlist Flight Mechanics

Progress in Geo Computation

From playlist Wolfram Technology Conference 2021

Franz Luef: Noncommutative geometry and time-frequency analysis

Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b

From playlist 30 years of wavelets

Live CEOing Ep 601: Language Design Review of Astronomy

From playlist Behind the Scenes in Real-Life Software Design

Implementing DeepMind's DQN from scratch! | Project Update

❤️ Become The AI Epiphany Patreon ❤️ ► https://www.patreon.com/theaiepiphany ▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬ I walk you through my project (it's still not working - RL of course it's not working!) and explain to you my workflow, how I think, organize my project, todos, etc. ▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬

From playlist Reinforcement Learning

How To Create A Video For Data Science Website Using Fusion | Session 02 | #design

Don’t forget to subscribe! In this project series, you will learn to create a video for a data science website using Fusion. This small course has the main goal to teach you how to use a node-based video editor Fusion from the Blackmagic Design team to create abstract video backgrounds

From playlist Create A Video For Data Science Website Using Fusion

Intro to GeoPandas

This is an introductory video to working with GeoPandas, using data pulled from Washing DC's Open Data page. We'll combine neighborhood polygons with construction permit point data to get permits per neighborhood per year, and create plots and maps with our results. Notebook in Githu

From playlist Introduction to GeoPandas

Isometry groups of the projective line (I) | Rational Geometry Math Foundations 138 | NJ Wildberger

The projective line can be given a Euclidean structure, just as the affine line can, but it is a bit more complicated. The algebraic structure of this projective line supports some symmetries. Symmetry in mathematics is often most efficiently encoded with the idea of a group--a technical t

From playlist Math Foundations

Projective frame

Related pages