The circle and projective homogeneous coordinates | Universal Hyperbolic Geometry 7a | NJ Wildberger
Universal hyperbolic geometry is based on projective geometry. This video introduces this important subject, which these days is sadly absent from most undergrad/college curriculums. We adopt the 19th century view of a projective space as the space of one-dimensional subspaces of an affine
From playlist Universal Hyperbolic Geometry

algebraic geometry 15 Projective space
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It introduces projective space and describes the synthetic and analytic approaches to projective geometry
From playlist Algebraic geometry I: Varieties

The circle and projective homogeneous coordinates (cont.) | Universal Hyperbolic Geometry 7b
Universal hyperbolic geometry is based on projective geometry. This video introduces this important subject, which these days is sadly absent from most undergrad/college curriculums. We adopt the 19th century view of a projective space as the space of one-dimensional subspaces of an affine
From playlist Universal Hyperbolic Geometry

Introduction to Projective Geometry (Part 1)
The first video in a series on projective geometry. We discuss the motivation for studying projective planes, and list the axioms of affine planes.
From playlist Introduction to Projective Geometry
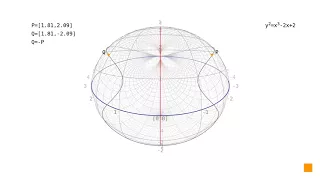
Elliptic curves: point at infinity in the projective plane
This video depicts point addition and doubling on elliptic curve in simple Weierstrass form in the projective plane depicted using stereographic projection where the point at infinity can actually be seen. Explanation is in the accompanying article https://trustica.cz/2018/04/05/elliptic-
From playlist Elliptic Curves - Number Theory and Applications

BAG2.2. Projective Toric Varieties - Part 2
Basic Algebraic Geometry: Continuing from the previous video, we give several equivalent conditions for when the cone over the projective toric variety X_A is equal to the affine toric variety Y_A.
From playlist Basic Algebraic Geometry

algebraic geometry 17 Affine and projective varieties
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It covers the relation between affine and projective varieties, with some examples such as a cubic curve and the twisted cubic.
From playlist Algebraic geometry I: Varieties

Zakhar Kabluchko: Random Polytopes, Lecture III
In these three lectures we will provide an introduction to the subject of beta polytopes. These are random polytopes defined as convex hulls of i.i.d. samples from the beta density proportional to (1 − ∥x∥2)β on the d-dimensional unit ball. Similarly, beta’ polytopes are defined as convex
From playlist Workshop: High dimensional spatial random systems
From playlist GeoGebra 3D

Nonlinear algebra, Lecture 7: "Toric Varieties", by Mateusz Michalek
This is the seventh lecture in the IMPRS Ringvorlesung, the advanced graduate course at the Max Planck Institute for Mathematics in the Sciences.
From playlist IMPRS Ringvorlesung - Introduction to Nonlinear Algebra

algebraic geometry 22 Toric varieties
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It describes toric varieties as examples of abstract varieties. For more about these see the book "Introduction to toric varieties" by Fulton.
From playlist Algebraic geometry I: Varieties

Spectrahedral lifts of convex sets – Rekha Thomas – ICM2018
Control Theory and Optimization Invited Lecture 16.6 Spectrahedral lifts of convex sets Rekha Thomas Abstract: Efficient representations of convex sets are of crucial importance for many algorithms that work with them. It is well-known that sometimes, a complicated convex set can be expr
From playlist Control Theory and Optimization

Positive cones of higher (co)dimensional numerical cycle classes - Mihai Fulger
Mihai Fulger Princeton University October 21, 2014 It is classical to study the geometry of projective varieties over algebraically closed fields through the properties of various positive cones of divisors or curves. Several counterexamples have shifted attention from the higher (co)dime
From playlist Mathematics
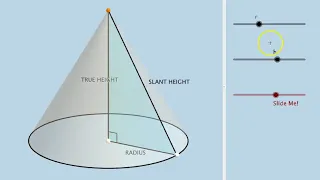
Right Circular Cone Anatomy: Quick Exploration
Engage here: https://www.geogebra.org/m/j9yyv3md
From playlist Geometry: Dynamic Interactives!

Lieven Vandenberghe: "Bregman proximal methods for semidefinite optimization."
Intersections between Control, Learning and Optimization 2020 "Bregman proximal methods for semidefinite optimization." Lieven Vandenberghe - University of California, Los Angeles (UCLA) Abstract: We discuss first-order methods for semidefinite optimization, based on non-Euclidean projec
From playlist Intersections between Control, Learning and Optimization 2020

Tropical Geometry - Lecture 11 - Toric Varieties | Bernd Sturmfels
Twelve lectures on Tropical Geometry by Bernd Sturmfels (Max Planck Institute for Mathematics in the Sciences | Leipzig, Germany) We recommend supplementing these lectures by reading the book "Introduction to Tropical Geometry" (Maclagan, Sturmfels - 2015 - American Mathematical Society)
From playlist Twelve Lectures on Tropical Geometry by Bernd Sturmfels

F. Polizzi - Classification of surfaces via Mori theory (Part 1)
We give a summary of the Minimal Model Program (namely, Mori Theory) in the case of surfaces.
From playlist Ecole d'été 2019 - Foliations and algebraic geometry

BAG2.1. Projective Toric Varieties - Part 1
Basic Algebraic Geometry: We define complex projective space, projective varieties, and projective toric varieties. For PTVs, we identify the character lattice and lattice of one-parameter subgroups.
From playlist Basic Algebraic Geometry

