Positive energy theorem

Theorems in general relativity

The positive energy theorem (also known as the positive mass theorem) refers to a collection of foundational results in general relativity and differential geometry. Its standard form, broadly speaking, asserts that the gravitational energy of an isolated system is nonnegative, and can only be zero when the system has no gravitating objects. Although these statements are often thought of as being primarily physical in nature, they can be formalized as mathematical theorems which can be proven using techniques of differential geometry, partial differential equations, and geometric measure theory. Richard Schoen and Shing-Tung Yau, in 1979 and 1981, were the first to give proofs of the positive mass theorem. Edward Witten, in 1982, gave the outlines of an alternative proof, which were later filled in rigorously by mathematicians. Witten and Yau were awarded the Fields medal in mathematics in part for their work on this topic. An imprecise formulation of the Schoen-Yau / Witten positive energy theorem states the following: Given an asymptotically flat initial data set, one can define the energy-momentum of each infinite region as an element of Minkowski space. Provided that the initial data set is geodesically complete and satisfies the dominant energy condition, each such element must be in the causal future of the origin. If any infinite region has null energy-momentum, then the initial data set is trivial in the sense that it can be geometrically embedded in Minkowski space. The meaning of these terms is discussed below. There are alternative and non-equivalent formulations for different notions of energy-momentum and for different classes of initial data sets. Not all of these formulations have been rigorously proven, and it is currently an open problem whether the above formulation holds for initial data sets of arbitrary dimension. (Wikipedia).

Positive Operators

Positive operators. Square roots of operators. Characterization of positive operators. Each positive operator has a unique positive square root.

From playlist Linear Algebra Done Right

Why Does a Negative Times a Negative Equal a Positive

This tutorial uses basic math and logic to demonstrate that a negative times a negative equals a positive. Join this channel to get access to perks: https://www.youtube.com/channel/UCn2SbZWi4yTkmPUj5wnbfoA/join :)

From playlist Basic Math

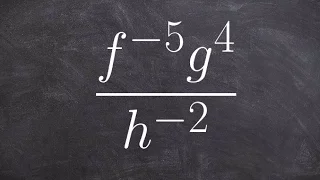
How do negative exponents simplify an expression

👉 Learn how to simplify expressions using the quotient rule and the negative exponent rule of exponents. The quotient rule of exponents states that the quotient of powers with a common base is equivalent to the power with the common base and an exponent which is the difference of the expon

From playlist Simplify Using the Rules of Exponents

Ex: Simplifying the Opposites of Negatives Integers

This video provides several examples of simplifying opposites of negative integers. Search Complete Video Library at http://www.mathispower4u.wordpress.com

From playlist Introduction to Integers

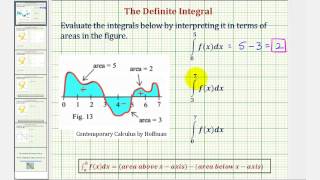
Ex: Definite Integrals as Area Given a Graph (Function)

This video explains how to evaluate a definite integral given the graph of a function and the area bounded by the function and the x-axis. The function is above and below the x-axis. Site: http://mathispower4u

From playlist Definite Integrals and The Fundamental Theorem of Calculus

Proving a Negative Times a Negative Is a Positive with the Distributive Property

When you're multiplying integers and especially when you begin multiplying negative numbers, one of the first questions that comes up for students is why does a negative times a negative equal a positive? There are lots of ways to show it, and a couple of my favorites are: + Multiplicatio

From playlist Math Mini

(ML 19.5) Positive semidefinite kernels (Covariance functions)

Definition of a positive semidefinite kernel, or covariance function. A simple example. Explanation of terminology: autocovariance, positive definite kernel, stationary kernel, isotropic kernel, covariogram, positive definite function.

From playlist Machine Learning

Cubic Curve Sketching (1 of 2: Using Factor Lines to determine regions the curve runs through)

More resources available at www.misterwootube.com

From playlist Further Work with Functions (related content)

Linear Algebra: Ch 2 - Determinants (7 of 48) Example of Rule 2: The Negative of a Determinant (2x2)

Visit http://ilectureonline.com for more math and science lectures! In this video I will show how to calculate the determinant of the negative of a determinant (2x2). (Rule 2) Next video in this series can be seen at: https://youtu.be/WWMb0c1Ttw8

From playlist LINEAR ALGEBRA 2: DETERMINANTS

Deriving the Work-Energy Theorem using Calculus

Use the integral and derivative to derive the Work-Energy Theorem or what I prefer to call the Net Work-Kinetic Energy Theorem. Want Lecture Notes? http://www.flippingphysics.com/wnet-ke.html This is an AP Physics 1 topic. 0:00 Intro 0:21 The integral definition of work 1:02 Net Work 1:53

From playlist Work, Energy, Power, Spring Force - AP Physics C: Mechanics

20/11/2015 - Richard Schoen - Localizing Solutions of the Einstein Equations

Abstract. In general it is not possible to localize solutions of the Einstein equations since there are asymptotic conserved quantities such as the total mass which are nonzero for every nontrivial space-time. In this lecture we will describe work with A. Carlotto which achieves a localiza

From playlist 2015-T3 - Mathematical general relativity - CEB Trimester

6.2 The Work-Energy Theorem and Kinetic Energy

This video covers Section 6.2 of Cutnell & Johnson Physics 10e, by David Young and Shane Stadler, published by John Wiley and Sons. The lecture is part of the course General Physics - Life Sciences I and II, taught by Dr. Boyd F. Edwards at Utah State University. This video was produced

From playlist Lecture 6A. Work and Energy

16: Particle orbits and Virial theorem - Part 2

Jacob Linder: 02.02.2012, Classical Mechanics (TFY454), v2012, NTNU A full textbook covering the material in the lectures in detail can be downloaded for free here: http://bookboon.com/en/introduction-to-lagrangian-hamiltonian-mechanics-ebook

From playlist NTNU: TFY 4345 - Classical Mechanics | CosmoLearning Physics

Denis Serre - Tenseurs symétriques positifs à divergence nulle. Applications.

From playlist Des mathématiciens primés par l'Académie des Sciences 2017

Harmonic maps into singular spaces - Brian Freidin

Variational Methods in Geometry Seminar Topic: Harmonic maps into singular spaces Speaker: Brian Freidin Affiliation: Brown University; Visitor, School of Mathematics Date: December 11, 2018 For more video please visit http://video.ias.edu

From playlist Variational Methods in Geometry

L2 curvature for surfaces in Riemannian manifolds - Ernst Kuwert

Workshop on Geometric Functionals: Analysis and Applications Topic: L2 curvature for surfaces in Riemannian manifolds Speaker: Ernst Kuwert Affiliation: University of Freiburg Date: March 7, 2019 For more video please visit http://video.ias.edu

From playlist Mathematics

[BOURBAKI 2017] 17/06/2017 - 3/4 - Frédéric ROUSSET

Solutions faibles de l'équation de Navier-Stokes des fluides compressibles [d'après A. Vasseur et C. Yu] ---------------------------------- Vous pouvez nous rejoindre sur les réseaux sociaux pour suivre nos actualités. Facebook : https://www.facebook.com/InstitutHenriPoincare/ Twitter :

From playlist BOURBAKI - 2017

Lecture 4 | Modern Physics: Statistical Mechanics

April 20, 2009 - Leonard Susskind explains how to calculate and define pressure, explores the formulas some of applications of Helm-Holtz free energy, and discusses the importance of the partition function. Stanford University: http://www.stanford.edu/ Stanford Continuing Studies P

From playlist Lecture Collection | Modern Physics: Statistical Mechanics

Ex: Comparing Absolute Value of Integers

This video provides three example of comparing integers and absolute value of integers using great than, less than, and equals. Search Complete Video Library at http://www.mathispower4u.wordpress.com

From playlist Absolute Value

Deriving the Heat Equation in 2D & 3D (& in N Dimensions!) with Control Volumes and Vector Calculus

Here we derive the heat equation in higher dimensions using Gauss's theorem. @eigensteve on Twitter eigensteve.com databookuw.com %%% CHAPTERS %%% 0:00 Overview 5:27 Heat Equation Derivation 11:45 Surface Integral to Volume Integral 15:04 Volume Integrals to PDEs

From playlist Engineering Math: Vector Calculus and Partial Differential Equations

Positive energy theorem

Related pages