
Tropical Quantum Field Theory, Mirror Polyvector Fields and Multiplicities... by Helge Ruddat
PROGRAM COMBINATORIAL ALGEBRAIC GEOMETRY: TROPICAL AND REAL (HYBRID) ORGANIZERS Arvind Ayyer (IISc, India), Madhusudan Manjunath (IITB, India) and Pranav Pandit (ICTS-TIFR, India) DATE 27 June 2022 to 08 July 2022 VENUE Madhava Lecture Hall and Online Algebraic geometry is the study of s
From playlist Combinatorial Algebraic Geometry: Tropical and Real (HYBRID)

[BOURBAKI 2017] 14/01/2017 - 3/4 - Maxim KONTSEVICH
Derived Grothendieck-Teichmüller group and graph complexes, after T. Willwacher Graph complex is spanned by equivalence classes of finite connected graphs with the dual differential given by the sum of all contractions of edges, with appropriate signs. This complex forms a differential g
From playlist BOURBAKI - 2017

Helge Ruddat: Factoring multiplicities of tropical curves
The lecture was held within the framework of the Hausdorff Trimester Program: Symplectic Geometry and Representation Theory. Abstract: Descendant log Gromov-Witten invariants of toric varieties match counts of tropical curves weighted by multiplicities that are obtained as indices of maps
From playlist HIM Lectures: Trimester Program "Symplectic Geometry and Representation Theory"

Twisted S-duality by Philsang Yoo
PROGRAM QUANTUM FIELDS, GEOMETRY AND REPRESENTATION THEORY 2021 (ONLINE) ORGANIZERS: Aswin Balasubramanian (Rutgers University, USA), Indranil Biswas (TIFR, india), Jacques Distler (The University of Texas at Austin, USA), Chris Elliott (University of Massachusetts, USA) and Pranav Pan
From playlist Quantum Fields, Geometry and Representation Theory 2021 (ONLINE)

Pre-recorded lecture 16: Frolicher-Nijenhuis bracket and Frolicher-Nijenhuis cohomology
MATRIX-SMRI Symposium: Nijenhuis Geometry and integrable systems Pre-recorded lecture: These lectures were recorded as part of a cooperation between the Chinese-Russian Mathematical Center (Beijing) and the Moscow Center of Fundamental and Applied Mathematics (Moscow). Nijenhuis Geomet
From playlist MATRIX-SMRI Symposium: Nijenhuis Geometry companion lectures (Sino-Russian Mathematical Centre)

👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

What is the definition of a regular polygon and how do you find the interior angles
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

What are four types of polygons
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

Classifying a polygon in two different ways ex 4
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

What are the names of different types of polygons based on the number of sides
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons
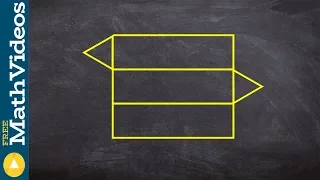
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

What is the difference between convex and concave
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

What is the difference between a regular and irregular polygon
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

Electromagnetism - Maxwell's Laws
Easy to understand 3D animation explaining all of Maxwell’s Equations. Includes explanations of induction motors, magnetic materials, electromagnetic waves, and many other topics.
From playlist Science

Dynamo theory and its application to the Sun by Arnab Rai Choudhuri
Turbulence from Angstroms to light years DATE:20 January 2018 to 25 January 2018 VENUE:Ramanujan Lecture Hall, ICTS, Bangalore The study of turbulent fluid flow has always been of immense scientific appeal to engineers, physicists and mathematicians because it plays an important role acr
From playlist Turbulence from Angstroms to light years

Electric field direction | Electric charge, field, and potential | Physics | Khan Academy
In this video David explains how to determine the direction of the electric field from positive and negative charges. He also shows how to determine the direction of the electric force on a charge in an electric field. Created by David SantoPietro. Watch the next lesson: https://www.khana
From playlist Electric charge, field, and potential | AP Physics 1 | Khan Academy

Understanding Quantum Field Theory
In a talk at Georgetown University, Dr. Rodney Brooks, author of "Fields of Color: The theory that escaped Einstein", shows why the answer is quantum field theory. He shows how quantum field theory, so often overlooked or misunderstood, resolves the weirdness of quantum mechanics and the
From playlist Quantum Field Theory

The Simple Rule Obeyed by All Electric Fields - Restrictions on the Field
Go to Squarespace.com for a free trial, and when you’re ready to launch, go to http://www.squarespace.com/parthg to save 10% off your first purchase of a website or domain. #electromagnetism #electricfield #maxwell #ad We can't just make up a vector field and assume such an electric fiel
From playlist Maxwell's Equations EXPLAINED

👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons