
What is a Bézier curve? Programmers use them everyday for graphic design, animation timing, SVG, and more. #shorts #animation #programming Animated Bézier https://www.jasondavies.com/animated-bezier/
From playlist CS101

In this video, I define connectedness, which is a very important concept in topology and math in general. Essentially, it means that your space only consists of one piece, whereas disconnected spaces have two or more pieces. I also define the related notion of path-connectedness. Topology
From playlist Topology

Akihiro Kanemitsu - Extremal rays and nefness of tangent bundles
May 8, 2016 - Princeton University This talk was part of the Princeton-Tokyo Algebraic Geometry Conference F. Campana and T. Peternell posed a problem to decide whether the tangent bundle of a Fano manifold is nef if the bundle is nef on every extremal rational curve. In this talk, we fir
From playlist Princeton-Tokyo Algebraic Geometry Conference
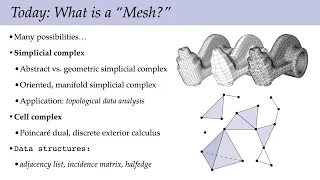
Lecture 2A: What is a "Mesh?" (Discrete Differential Geometry)
Full playlist: https://www.youtube.com/playlist?list=PL9_jI1bdZmz0hIrNCMQW1YmZysAiIYSSS For more information see http://geometry.cs.cmu.edu/ddg
From playlist Discrete Differential Geometry - CMU 15-458/858

Shapes and Solids of Constant Width - Numberphile
Get them at Maths Gear: http://bit.ly/mathsgear More links & stuff in full description below ↓↓↓ Steve Mould discusses shapes and solids of constant width, including the Reuleaux triangle and the UK's 50p coin. Brown papers: http://bit.ly/brownpapers NUMBERPHILE Website: http://www.numb
From playlist Festival of Spoken Nerd on Numberphile

Arend Bayer : Stability and applications to birational and hyperkaehler geometry - lecture 2
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebraic and Complex Geometry

Featuring Joe Buhler. See part 2 of this interview: https://youtu.be/4YG4QnhVV7A More links & stuff in full description below ↓↓↓ An Introduction to Infinite Hat Problems (paper): https://bit.ly/31OeWZK See also Spheres and Code Words with James Grime: https://youtu.be/T46FTuHnbvY Numb
From playlist Infinity on Numberphile

Cécile Gachet : Positivity of higher exterior powers of the tangent bundle
CONFERENCE Recording during the thematic meeting : "Algebraic Geometry and Complex Geometry " the December1, 2022 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Jean Petit Find this video and other talks given by worldwide mathematicians on CIRM's
From playlist Algebraic and Complex Geometry

Nef Reaction (Introduction to Umpolung Chemistry)
The Nef reaction is a good way to convert nitronates into carbonyl compounds. This is a technique that can be incorporated into a strategy called "Umpolung", which refers to a reversal of polarity, such that upon converting from the nitronate to the carbonyl after some addition has occurre
From playlist Organic Chemistry

Geometric Algebra - Rotors and Quaternions
In this video, we will take note of the even subalgebra of G(3), see that it is isomorphic to the quaternions and, in particular, the set of rotors, themselves in the even subalgebra, correspond to the set of unit quaternions. This brings the entire subject of quaternions under the heading
From playlist Math

Arend Bayer: Stability and applications to birational and hyperkaehler geometry - lecture 1
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebraic and Complex Geometry

V. Tosatti - $C^{1,1}$ estimates for complex Monge-Ampère equations
I will discuss a method that we recently introduced in collaboration with Chu and Weinkove which gives interior C1,1 estimates for the non-degenerate complex Monge-Ampère equation on compact Kähler manifolds (possibly with boundary). The method is sufficiently robust to also give C1,1 regu
From playlist Complex analytic and differential geometry - a conference in honor of Jean-Pierre Demailly - 6-9 juin 2017
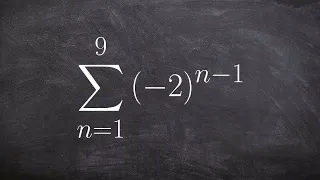
Find the partial sum of the geometric series
👉 Learn how to find the geometric sum of a series. A series is the sum of the terms of a sequence. A geometric series is the sum of the terms of a geometric sequence. The formula for the sum of n terms of a geometric sequence is given by Sn = a[(r^n - 1)/(r - 1)], where a is the first term
From playlist Series

Arend Bayer: Stability and applications to birational and hyperkaehler geometry - lecture 3
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebraic and Complex Geometry

S. Druel - A decomposition theorem for singular spaces with trivial canonical class (Part 5)
The Beauville-Bogomolov decomposition theorem asserts that any compact Kähler manifold with numerically trivial canonical bundle admits an étale cover that decomposes into a product of a torus, an irreducible, simply-connected Calabi-Yau, and holomorphic symplectic manifolds. With the deve
From playlist Ecole d'été 2019 - Foliations and algebraic geometry

The Henry reaction is sometimes called a nitroaldol reaction, because it involves the addition of a nitronate salt to a carbonyl compound. This is a great setup for a Nef reaction, which was learned in the previous tutorial. Let's look at the mechanism and some important applications, incl
From playlist Organic Chemistry

2022 10 Dan Coman: Extension of quasiplurisubharmonic functions
CONFERENCE Recording during the thematic meeting : "Complex Geometry, Dynamical Sytems and Foliation Theory" the October 20, 2022 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Jean Petit Find this video and other talks given by worldwide mathemat
From playlist Analysis and its Applications

I will introduce the tangent bundle of a smooth manifold, from the point of view of function calculus on a manifold. At the end I show that the tangent bundle is a smooth manifold. A good reference to learn this is do Carmo's "Differential Forms and Applications" Chapter 3. Please like a
From playlist Differential geometry

