
Schemes 42: Very ample sheaves
This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne. We define ample and very ample invertible sheaves for projective varieties, and gives some examples for complex elliptic curves. We also show that some sect
From playlist Algebraic geometry II: Schemes

Abstract Algebra | Injective Functions
We give the definition of an injective function, an outline of proving that a given function is injective, and a few examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Schemes 29: Invertible sheaves over the projective line
This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne. In this lecture we classify the invertible sheaves over the projective line, and use them to show that several properties of quasiprojective sheaves over affi
From playlist Algebraic geometry II: Schemes

Description: Corresponding to our algebraic notion of invertibility, we want a geometric notion. Invertible transformations are defined, and then proven to be equivalent (thank goodness!) to invertible matrices when linear. Learning Objectives: 1) Define an invertible transformation 2) D
From playlist Older Linear Algebra Videos

Invertibility and Isomorphic Vector Spaces
The dimension of L(V, W). Linear maps act like matrix multiplication. Injectivity is equivalent to surjectivity in finite dimensions.
From playlist Linear Algebra Done Right

What is an Injective Function? Definition and Explanation
An explanation to help understand what it means for a function to be injective, also known as one-to-one. The definition of an injection leads us to some important properties of injective functions! Subscribe to see more new math videos! Music: OcularNebula - The Lopez
From playlist Functions

Definition of an Injective Function and Sample Proof
We define what it means for a function to be injective and do a simple proof where we show a specific function is injective. Injective functions are also called one-to-one functions. Useful Math Supplies https://amzn.to/3Y5TGcv My Recording Gear https://amzn.to/3BFvcxp (these are my affil
From playlist Injective, Surjective, and Bijective Functions
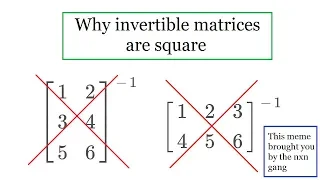
Invertible matrices are square
Why invertible matrices must be square. Definition of invertible matrix and showing that a 3x2 and a 2x3 matrix cannot be square. Check out my Matrix Algebra playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmAIZGo2l8SWvsHeeCLzamx0 Subscribe to my channel: https://www.youtube.c
From playlist Matrix Algebra

The Composition of Injective(one-to-one) Functions is Injective Proof
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Proof that the composition of injective(one-to-one) functions is also injective(one-to-one)
From playlist Proofs

Georg Biedermann - Higher Sheaves
Talk at the school and conference “Toposes online” (24-30 June 2021): https://aroundtoposes.com/toposesonline/ Joint work with Mathieu Anel, Eric Finster, and André Joyal Even though on the surface the theories look similar, there are basic differences between the classical theory of 1-t
From playlist Toposes online

Schemes 45: Blowing up schemes
This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne. In this lecture we discuss the operation of blowing up a scheme along a sheaf of ideals. This can be used to make ideals invertible, and to eliminate points o
From playlist Algebraic geometry II: Schemes

Marc Levine: The rational motivic sphere spectrum and motivic Serre finiteness
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist SPECIAL 7th European congress of Mathematics Berlin 2016.

Schemes 38: Comparison of Cartier divisors and Pic
This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne. In this lecture we Define a homomorphism from Caritier divisor classes to the Picard group, and show that it is an isomorphism for integral schemes. We use thi
From playlist Algebraic geometry II: Schemes

Matthew Morrow: Relative integral p-adic Hodge theory
Abstract: Given a smooth scheme X over the ring of integers of a p-adic field, we introduce the notion of a relative Breuil-Kisin-Fargues module M on X. Each such M simultaneously encodes the data of a lisse étale sheaf, a module with flat connection, and a crystal, whose cohomologies are
From playlist Algebraic and Complex Geometry

Emily Cliff: Hilbert Schemes Lecture 3
SMRI Seminar Series: 'Hilbert Schemes' Lecture 3 The universal family on H Emily Cliff (University of Sydney) This series of lectures aims to present parts of Nakajima’s book `Lectures on Hilbert schemes of points on surfaces’ in a way that is accessible to PhD students interested in rep
From playlist SMRI Course: Hilbert Schemes

Schemes 5: Definition of a scheme
This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne. We give some historical background, then give the definition of a scheme and some simple examples, and finish by explaining the origin of the word "spectrum".
From playlist Algebraic geometry II: Schemes

From Cohomology to Derived Functors by Suresh Nayak
PROGRAM DUALITIES IN TOPOLOGY AND ALGEBRA (ONLINE) ORGANIZERS: Samik Basu (ISI Kolkata, India), Anita Naolekar (ISI Bangalore, India) and Rekha Santhanam (IIT Mumbai, India) DATE & TIME: 01 February 2021 to 13 February 2021 VENUE: Online Duality phenomena are ubiquitous in mathematics
From playlist Dualities in Topology and Algebra (Online)

Duality in Algebraic Geometry by Suresh Nayak
PROGRAM DUALITIES IN TOPOLOGY AND ALGEBRA (ONLINE) ORGANIZERS: Samik Basu (ISI Kolkata, India), Anita Naolekar (ISI Bangalore, India) and Rekha Santhanam (IIT Mumbai, India) DATE & TIME: 01 February 2021 to 13 February 2021 VENUE: Online Duality phenomena are ubiquitous in mathematics
From playlist Dualities in Topology and Algebra (Online)
Étale cohomology lecture 3, August 27, 2020
Sites and sheaves, the étale and fppf site, representable functors
From playlist Étale cohomology and the Weil conjectures

Who Gives a Sheaf? Part 1: A First Example
We take a first look at (pre-)sheaves, as being inspired from first year calculus.
From playlist Who Gives a Sheaf?