
Commutative algebra 35 Nakayama's lemma
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. This lecture is about Nakayama's lemma, which states that if M is a finitely generated module over a local ring with maximal i
From playlist Commutative algebra

This lecture is part of an online course on categories. Any object of a category can be thought of as a representable functor in the category of presheaves. We give several examples of representable functors. Then we state Yoneda's lemma, which roughly that morphisms of objects are he sa
From playlist Categories for the idle mathematician

Nakayama's Lemma - April 12 2021
This is a video from by Abstract Algebra 4 course that took place in Spring 2021.
From playlist Course on Rings and Modules (Abstract Algebra 4) [Graduate Course]

Andrei Okounkov - Nakajima Varieties
April 4, 2014 - This is the 6th of 10 Minerva Distinguished Visitor Lectures at the Princeton University Mathematics Department. Nakajima varieties are very remarkable algebraic symplectic varieties that can be associated to an arbitrary multigraph (which later in the theory plays the ro
From playlist Minerva Mini Course - Andrei Okounkov

Commutative algebra 36 Artin Rees lemma
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. In this lecture we state and prove the Artin-Rees lemma, which states that the restriction of an stable I-adic filtration (of
From playlist Commutative algebra

Commutative algebra 44 Flat modules
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. We summarize some of the properties of flat modules. In particular we show that for finitely presented modules over local ring
From playlist Commutative algebra

Andrei Okounkov - Geometric R-matrices for Nakajima varieties, II
April 18, 2014 - Princeton University Department of Mathematics This is the 7th of 10 Minerva Distinguished Visitor Lectures. Part II: this week, we will begin to merge the discussion of stable envelopes and Nakajima varieties to produce a geometric action of a certain Yangian on equivar
From playlist Minerva Mini Course - Andrei Okounkov
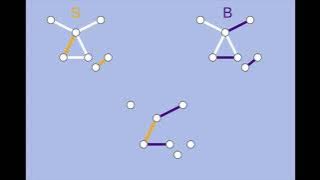
Berge's lemma, an animated proof
Berge's lemma is a mathematical theorem in graph theory which states that a matching in a graph is of maximum cardinality if and only if it has no augmenting paths. But what do those terms even mean? And how do we prove Berge's lemma to be true? == CORRECTION: at 7:50, the red text should
From playlist Summer of Math Exposition Youtube Videos

Schemes 42: Very ample sheaves
This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne. We define ample and very ample invertible sheaves for projective varieties, and gives some examples for complex elliptic curves. We also show that some sect
From playlist Algebraic geometry II: Schemes

The Bible of Abstract Algebra If you knew everything in this book you would be a MATH GOD! This is absolutely the most comprehensive abstract algebra book in the ENTIRE WORLD. You can see it here on amazon: https://amzn.to/31I3Lhz (note this is my affiliate link, I earn a small percentag
From playlist Cool Math Stuff

Localization of Primary Ideals - April 23 and 26, 2021
Errata: in the very last part, we need to assume that x1 in not in P1 not just Q1.
From playlist Course on Rings and Modules (Abstract Algebra 4) [Graduate Course]

Cayley Hamilton - April 09 2021
This is for my abstract algebra 4 course.
From playlist Course on Rings and Modules (Abstract Algebra 4) [Graduate Course]

Olivier Taïbi - 3/3 The Local Langlands Conjecture
We formulate the local Langlands conjecture for connected reductive groups over local fields, including the internal parametrization of L-packets. Olivier Taïbi (ENS Lyon)
From playlist 2022 Summer School on the Langlands program
Packaging the construction of Kuranishi structure - Kenji Fukaya
Princeton/IAS Symplectic Geometry Seminar Topic: Packaging the construction of Kuranishi structure on the moduli space of pseudo-holomorphic curve Speaker: Kenji Fukaya Affiliation: Stonybrook University Date: October 4, 2016
From playlist Mathematics

A. Höring - A decomposition theorem for singular spaces with trivial canonical class (Part 3)
The Beauville-Bogomolov decomposition theorem asserts that any compact Kähler manifold with numerically trivial canonical bundle admits an étale cover that decomposes into a product of a torus, an irreducible, simply-connected Calabi-Yau, and holomorphic symplectic manifolds. With the deve
From playlist Ecole d'été 2019 - Foliations and algebraic geometry

Hiraku Nakajima - Ring objects in the derived Satake category from Coulomb branches
Abstract: In my joint work with Braverman and Finkelberg, we proposed a mathematical definition of Coulomb branches of SUSY gauge theories as Borel-Moore homology of certain varieties which have maps to affine Grassmannians. This construction gives ring objects in derived Satake categorie
From playlist Algebraic Analysis in honor of Masaki Kashiwara's 70th birthday

