Powered by https://www.numerise.com/ Gradient of a line segment 1
From playlist Linear sequences & straight lines

See also https://youtu.be/BYTi0RWp494 and https://youtu.be/vV_vIFL3LKU
From playlist gradient_descent
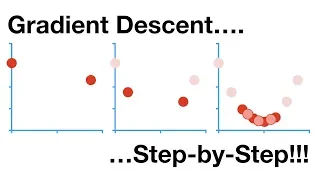
Gradient Descent, Step-by-Step
Gradient Descent is the workhorse behind most of Machine Learning. When you fit a machine learning method to a training dataset, you're probably using Gradient Descent. It can optimize parameters in a wide variety of settings. Since it's so fundamental to Machine Learning, I decided to mak
From playlist Optimizers in Machine Learning

This video follows on from the discussion on linear regression as a shallow learner ( https://www.youtube.com/watch?v=cnnCrijAVlc ) and the video on derivatives in deep learning ( https://www.youtube.com/watch?v=wiiPVB9tkBY ). This is a deeper dive into gradient descent and the use of th
From playlist Introduction to deep learning for everyone

Sean Kafer: Performance of steepest descent in 0/1 LPs
Even after decades of study, it is unknown whether there exists a pivot rule for the Simplex method that always solves an LP with only a polynomial number of pivots. This remains unknown even in the special case of 0/1 LPs, a case that includes many extensively studied problems in combinat
From playlist Workshop: Tropical geometry and the geometry of linear programming

Numerical Optimization Algorithms: Gradient Descent
In this video we discuss a general framework for numerical optimization algorithms. We will see that this involves choosing a direction and step size at each step of the algorithm. In this video, we investigate how to choose a direction using the gradient descent method. Future videos d
From playlist Optimization

Introduction to Gradient Descent
An introduction to gradient descent. See also https://youtu.be/W2pSn_t0KYs
From playlist gradient_descent

11. Unconstrained Optimization; Newton-Raphson and Trust Region Methods
MIT 10.34 Numerical Methods Applied to Chemical Engineering, Fall 2015 View the complete course: http://ocw.mit.edu/10-34F15 Instructor: James Swan Students learned how to solve unconstrained optimization problems. In addition of the Newton-Raphson method, students also learned the steepe
From playlist MIT 10.34 Numerical Methods Applied to Chemical Engineering, Fall 2015

Lecture 15 | Convex Optimization I (Stanford)
Professor Stephen Boyd, of the Stanford University Electrical Engineering department, lectures on how unconstrained minimization can be used in electrical engineering and convex optimization for the course, Convex Optimization I (EE 364A). Convex Optimization I concentrates on recognizi
From playlist Lecture Collection | Convex Optimization

Jorge Nocedal: "Tutorial on Optimization Methods for Machine Learning, Pt. 1"
Graduate Summer School 2012: Deep Learning, Feature Learning "Tutorial on Optimization Methods for Machine Learning, Pt. 1" Jorge Nocedal, Northwestern University Institute for Pure and Applied Mathematics, UCLA July 19, 2012 For more information: https://www.ipam.ucla.edu/programs/summ
From playlist GSS2012: Deep Learning, Feature Learning

Optimisation - an introduction: Professor Coralia Cartis, University of Oxford
Coralia Cartis (BSc Mathematics, Babesh-Bolyai University, Romania; PhD Mathematics, University of Cambridge (2005)) has joined the Mathematical Institute at Oxford and Balliol College in 2013 as Associate Professor in Numerical Optimization. Previously, she worked as a research scientist
From playlist Data science classes

QED Prerequisites Scattering 6
In this lesson we review some critical mathematics associated with complex analysis. In particular, the nature of an analytic function, the Cauchy Integral Theorem, and the maximum modulus theorem. After this review we turn back to the dark art of asymptotic analysis and study the very cle
From playlist QED- Prerequisite Topics

Stephen Wright: "Some Relevant Topics in Optimization, Pt. 2"
Graduate Summer School 2012: Deep Learning Feature Learning "Some Relevant Topics in Optimization, Pt. 2" Stephen Wright, University of Wisconsin-Madison Institute for Pure and Applied Mathematics, UCLA July 16, 2012 For more information: https://www.ipam.ucla.edu/programs/summer-school
From playlist GSS2012: Deep Learning, Feature Learning

Jorge Nocedal: "Tutorial on Optimization Methods for Machine Learning, Pt. 2"
Graduate Summer School 2012: Deep Learning, Feature Learning "Tutorial on Optimization Methods for Machine Learning, Pt. 2" Jorge Nocedal, Northwestern University Institute for Pure and Applied Mathematics, UCLA July 19, 2012 For more information: https://www.ipam.ucla.edu/programs/summ
From playlist GSS2012: Deep Learning, Feature Learning
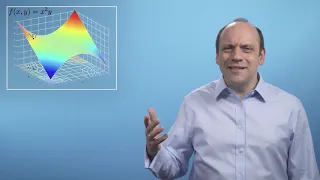
M4ML - Multivariate Calculus - 5.2 Gradient Descent
Welcome to the “Mathematics for Machine Learning: Multivariate Calculus” course, offered by Imperial College London. This video is part of an online specialisation in Mathematics for Machine Learning (m4ml) hosted by Coursera. For more information on the course and to access the full ex
From playlist Mathematics for Machine Learning - Multivariate Calculus

Lec 19 | MIT 18.086 Mathematical Methods for Engineers II
Conjugate Gradient Method View the complete course at: http://ocw.mit.edu/18-086S06 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 18.086 Mathematical Methods for Engineers II, Spring '06

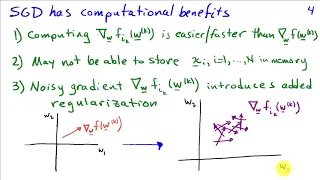
Stochastic Gradient Descent, Clearly Explained!!!
Even though Stochastic Gradient Descent sounds fancy, it is just a simple addition to "regular" Gradient Descent. This video sets up the problem that Stochastic Gradient Descent solves and then shows how it does it. Along the way, we discuss situations where Stochastic Gradient Descent is
From playlist StatQuest