
Using a Matrix Equation to Solve a System of Equations
This video shows how to solve a system of equations by using a matrix equation. The graphing calculator is integrated into the lesson. http://mathispower4u.yolasite.com/ http://mathispower4u.wordpress.com/
From playlist Matrix Equations

Ex 2: Solve a System of Two Equations Using a Matrix Equation
This video explains how to solve a system of two linear equations with two unknowns using a matrix equation. Site: http://mathispower4u Blog: http://mathispower4u.wordpress.com
From playlist Matrix Equations

Ex: Write a System of Equations as a Matrix Equation (3x3)
This video explains how to write a matrix equation for a system of three equations with three unknowns. http://mathispower4u.com
From playlist Matrix Equations

Solving a System of Equations with a Matrix Equation
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Quick video on how to solve a system of equations with matrix equation.
From playlist Systems of Equations

Ex 1: Solve a System of Two Equations Using a Matrix Equation
This video explains how to solve a system of two linear equations with two unknowns using a matrix equation. Site: http://mathispower4u Blog: http://mathispower4u.wordpress.com
From playlist Matrix Equations

Ex: Solve a Basic Matrix Equation (No Inverse)
This video explains how to solve a basic matrix equation. No inverse matrix is needed. http://mathispower4u.com
From playlist Introduction to Matrices and Matrix Operations

Ex: Solve a System of Three Equations Using a Matrix Equation
This video explains how to solve a system of three linear equations with three unknowns using a matrix equation. Site: http://mathispower4u Blog: http://mathispower4u.wordpress.com
From playlist Matrix Equations

Linear Algebra - Lecture 9 - Matrix Equations
In this lecture, we define the product of a matrix by a vector. We also discuss matrix equations and their connection to systems of linear equations and vector equations.
From playlist Linear Algebra Lectures

Matrix Addition, Subtraction, and Scalar Multiplication
This video shows how to add, subtract and perform scalar multiplication with matrices. http://mathispower4u.yolasite.com/ http://mathispower4u.wordpress.com/
From playlist Introduction to Matrices and Matrix Operations
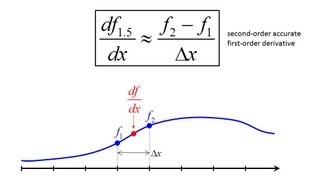
Lecture 9 (CEM) -- Finite-Difference Method
This lecture introduces the student to the finite-difference method and how we will implement it in this class using matrix operators. The lectures ends by providing a number of examples of derivative operators on different size grids.
From playlist UT El Paso: CEM Lectures | CosmoLearning.org Electrical Engineering

Lec 11 | MIT RES.6-008 Digital Signal Processing, 1975
Lecture 11: Representation of linear digital networks Instructor: Alan V. Oppenheim View the complete course: http://ocw.mit.edu/RES6-008S11 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT RES.6-008 Digital Signal Processing, 1975

Lecture 19 (CEM) -- Formulation of Rigorous Coupled-Wave Analysis
This lecture steps the student through the formulation of rigorous coupled-wave analysis. It parallels the lecture on the transfer matrix method and adopts the same formalism for scattering matrices. A bonus section discusses the enhanced transmittance matrix approach. Prerequisite Lect
From playlist UT El Paso: CEM Lectures | CosmoLearning.org Electrical Engineering

Lecture 5 (CEM) -- TMM Using Scattering Matrices
This lecture formulates a stable transfer matrix method based on scattering matrices. The scattering matrices adopted here are greatly improved from the literature and are consistent with convention. The lecture ends with some advanced topics like dispersion analysis, cascading and doubl
From playlist UT El Paso: CEM Lectures | CosmoLearning.org Electrical Engineering

17: Principal Components Analysis_ - Intro to Neural Computation
MIT 9.40 Introduction to Neural Computation, Spring 2018 Instructor: Michale Fee View the complete course: https://ocw.mit.edu/9-40S18 YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP61I4aI5T6OaFfRK2gihjiMm Covers eigenvalues and eigenvectors, Gaussian distributions, co
From playlist MIT 9.40 Introduction to Neural Computation, Spring 2018

Valeria Simoncini: Computational methods for large-scale matrix equations and application to PDEs
Linear matrix equations such as the Lyapunov and Sylvester equations and their generalizations have classically played an important role in the analysis of dynamical systems, in control theory and in eigenvalue computation. More recently, matrix equations have emerged as a natural linear a
From playlist Numerical Analysis and Scientific Computing

Basic Lectures on Bethe Ansatz (Pedagogical Lecture 03) by Fabio Franchini
PROGRAM: INTEGRABLE SYSTEMS IN MATHEMATICS, CONDENSED MATTER AND STATISTICAL PHYSICS ORGANIZERS: Alexander Abanov, Rukmini Dey, Fabian Essler, Manas Kulkarni, Joel Moore, Vishal Vasan and Paul Wiegmann DATE : 16 July 2018 to 10 August 2018 VENUE: Ramanujan Lecture Hall, ICTS Bangalore
From playlist Integrable systems in Mathematics, Condensed Matter and Statistical Physics

5. Eigenvalues and Eigenvectors
MIT 10.34 Numerical Methods Applied to Chemical Engineering, Fall 2015 View the complete course: http://ocw.mit.edu/10-34F15 Instructor: James Swan Examples were presented to demonstrate how to find eigenvalues and eigenvectors of a matrix and explain their properties. License: Creative
From playlist MIT 10.34 Numerical Methods Applied to Chemical Engineering, Fall 2015

Lecture 24 (CEM) -- Introduction to Variational Methods
This lecture introduces to the student to variational methods including finite element method, method of moments, boundary element method, and spectral domain method. It describes the Galerkin method for transforming a linear equation into matrix form as well as populating the global matr
From playlist UT El Paso: CEM Lectures | CosmoLearning.org Electrical Engineering

How to Find Eigenvalues of a Matrix
This video explains how to find the eigenvalues of a given matrix.
From playlist Eigenvalues and Eigenvectors

(3.2.4B) Solving a System of Linear Equations Using a Matrix Equation
This lesson explains how to solve a system of equations using a matrix equation. https://mathispower4u.com
From playlist Differential Equations: Complete Set of Course Videos