
Powered by https://www.numerise.com/ C1 Sequences & Series (1)
From playlist Core 1 - Sequences and Series

What is the alternate in sign sequence
👉 Learn about sequences. A sequence is a list of numbers/values exhibiting a defined pattern. A number/value in a sequence is called a term of the sequence. There are many types of sequence, among which are: arithmetic and geometric sequence. An arithmetic sequence is a sequence in which
From playlist Sequences

👉 Learn about sequences. A sequence is a list of numbers/values exhibiting a defined pattern. A number/value in a sequence is called a term of the sequence. There are many types of sequence, among which are: arithmetic and geometric sequence. An arithmetic sequence is a sequence in which
From playlist Sequences

Finding the first four terms of a sequence given a factorial
👉 Learn how to find the first five terms of a sequence. Given an explicit formula for a sequence, we can find the nth term of the sequence by plugging the term number of the sequence for n in the given formula. When n = 1, 2, . . ., 5 are plugged into the explicit formula, we obtain the fi
From playlist Sequences

What is the definition of a geometric sequence
👉 Learn about sequences. A sequence is a list of numbers/values exhibiting a defined pattern. A number/value in a sequence is called a term of the sequence. There are many types of sequence, among which are: arithmetic and geometric sequence. An arithmetic sequence is a sequence in which
From playlist Sequences

What is the difference between finite and infinite sequences
👉 Learn about sequences. A sequence is a list of numbers/values exhibiting a defined pattern. A number/value in a sequence is called a term of the sequence. There are many types of sequence, among which are: arithmetic and geometric sequence. An arithmetic sequence is a sequence in which
From playlist Sequences
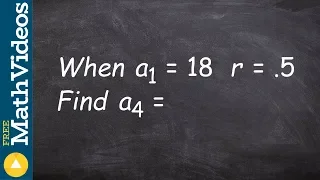
Learn to write the explicit formula for the geometric sequence
👉 Learn how to write the explicit formula for a geometric sequence. A sequence is a list of numbers/values exhibiting a defined pattern. A number/value in a sequence is called a term of the sequence. A geometric sequence is a sequence in which each term of the sequence is obtained by multi
From playlist Sequences

What is the recursive formula and how do we use it
👉 Learn about sequences. A sequence is a list of numbers/values exhibiting a defined pattern. A number/value in a sequence is called a term of the sequence. There are many types of sequence, among which are: arithmetic and geometric sequence. An arithmetic sequence is a sequence in which
From playlist Sequences

This video introduces sequences. http://mathispower4u.yolasite.com/
From playlist Infinite Series

Part Three of Golden Ratio Trilogy Why the Lucas Numbers are better than the Fibonacci Sequence. More links & stuff in full description below ↓↓↓ Matt's signed book (& extra goodies): http://bit.ly/Matt_Signed Amazon (UK): http://bit.ly/Matt_4D_UK Amazon (US): http://bit.ly/Matt_4D_US Al
From playlist Matt Parker (standupmaths) on Numberphile
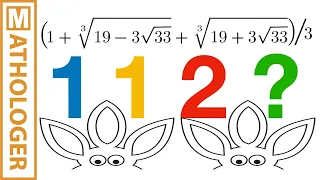
Phi and the TRIBONACCI monster
NEW (Christmas 2019). Two ways to support Mathologer Mathologer Patreon: https://www.patreon.com/mathologer Mathologer PayPal: paypal.me/mathologer (see the Patreon page for details) Today's video is about explaining a lot of the miracles associated with the golden ratio phi, the Fibona
From playlist Recent videos

Golden Ratio BURN (Internet Beef) - Numberphile
Seriously? Matt Parker is talking about Fibonacci and Lucas numbers again. Part 2: https://youtu.be/z1THaBtc5RE More links & stuff in full description below ↓↓↓ See part 2 on Numberphile2: https://youtu.be/z1THaBtc5RE The original trilogy of videos where this all started: http://bit.ly/G
From playlist Matt Parker (standupmaths) on Numberphile

How they found the World's Biggest Prime Number - Numberphile
Featuring Matt Parker... More links & stuff in full description below ↓↓↓ See part one at: https://youtu.be/tlpYjrbujG0 Part three on Numberphile2: https://youtu.be/jNXAMBvYe-Y Matt's interview with Curtis Cooper: https://youtu.be/q5ozBnrd5Zc The previous record: https://youtu.be/QSEKzFG
From playlist Matt Parker (standupmaths) on Numberphile

Norm Form Equations and Linear Divisibility Sequences (CTNT 2020)
Contact Information: Elisa Bellah ebellah@uoregon.edu pages.uoregon.edu/ebellah Abstract: Finding integer solutions to norm form equations is a classic Diophantine problem. Using the units of the associated coefficient ring, we can produce sequences of solutions to these equations. It tur
From playlist CTNT 2020 - Conference Videos

Discrete Structures: Multiplicative inverse, Euler's totient function, and Euler's theorem
This is a continuation of the previous live stream session. Learn more about Euler's totient function and how we can use it, along with Euler's theorem, to compute the multiplicative inverse of any number (a mod n). We'll also learn about the extended Euclidean algorithm to compute the mul
From playlist Discrete Structures, Spring 2022

Nice Little Linear Algebra Problem from a Fibonacci-esque Sequence
I got this problem from an old U.I.L. Mathematics competition (high school level): given a Fibonacci characteristic sequence …3, p, q, 5, r…, what is p+q+r? Subscribe: https://bit.ly/polymathematic | Enable ALL push notifications 🔔 Not the world's hardest problem, but there are some clev
From playlist Math Mini

The AI Buzz, Episode #1: ChatGPT, Transformers and Attention
The AI Buzz is a conversation about the latest trends in AI, plus Q&A, between me and Luca Antiga, the Chief Technology Officer at Lightning AI. We talk about what's new and why it has the potential to change everything. And, because it's StatQuest, we'll go the extra mile to make sure eve
From playlist The AI Buzz with Luca and Josh

Write the first five terms of a sequence with factorials
👉 Learn how to find the first five terms of a sequence. Given an explicit formula for a sequence, we can find the nth term of the sequence by plugging the term number of the sequence for n in the given formula. When n = 1, 2, . . ., 5 are plugged into the explicit formula, we obtain the fi
From playlist Sequences

The Last Universal Common Ancestor ft. Times Infinity
What was the Last Universal Common Ancestor If we trace back our ancestor its quickly revealed at some point the number of ancestors starts to exceed the population of earth at the time, eventually you can trace everything back to one organism, from which all currently alive things are de
From playlist Collaborations
