
Modular Forms | Modular Forms; Section 1 2
We define modular forms, and borrow an idea from representation theory to construct some examples. My Twitter: https://twitter.com/KristapsBalodi3 Fourier Theory (0:00) Definition of Modular Forms (8:02) In Search of Modularity (11:38) The Eisenstein Series (18:25)
From playlist Modular Forms

Modular forms: Eisenstein series
This lecture is part of an online graduate course on modular forms. We give two ways of looking at modular forms: as functions of lattices in C, or as invariant forms. We use this to give two different ways of constructing Eisenstein series. For the other lectures in the course see http
From playlist Modular forms

Number Theory | Modular Inverses: Example
We give an example of calculating inverses modulo n using two separate strategies.
From playlist Modular Arithmetic and Linear Congruences

Modular Exponentiation Quiz - Applied Cryptography
This video is part of an online course, Applied Cryptography. Check out the course here: https://www.udacity.com/course/cs387.
From playlist Applied Cryptography

This lecture is part of an online graduate course on modular forms. We introduce modular forms, and give several examples of how they were used to solve problems in apparently unrelated areas of mathematics. I will not be following any particular book, but if anyone wants a suggestion
From playlist Modular forms

Applying the rules of exponents to simplify an expression with numbers
👉 Learn about the rules of exponents. An exponent is a number which a number is raised to, to produce a power. It is the number of times which a number will multiply itself in a power. There are several rules used in evaluating exponents. Some of the rules includes: the product rule, which
From playlist Simplify Using the Rules of Exponents
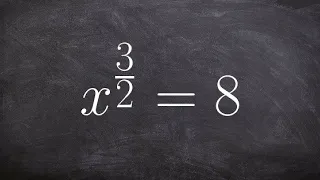
How to solve an equation with fraction powers in your exponent
👉 Learn how to deal with Rational Powers or Exponents. Exponents are shorthand for repeated multiplication of the same thing by itself. This process of using exponents is called "raising to a power", where the exponent is the "power". Rational exponents are exponents that are fractions. To
From playlist Solve Equations with Fractional Exponents

How Does the Rules of Exponents Allows to Multiply and Divide by Monomials
👉 Learn about the rules of exponents. An exponent is a number which a number is raised to, to produce a power. It is the number of times which a number will multiply itself in a power. There are several rules used in evaluating exponents. Some of the rules includes: the product rule, which
From playlist Simplify Using the Rules of Exponents

Simplifying Expressions by Using the Product Rule of Exponents
👉 Learn about the rules of exponents. An exponent is a number which a number is raised to, to produce a power. It is the number of times which a number will multiply itself in a power. There are several rules used in evaluating exponents. Some of the rules includes: the product rule, which
From playlist Simplify Using the Rules of Exponents

Compatibility of Explicit Reciprocity Laws by Shanwen Wang
Program Recent developments around p-adic modular forms (ONLINE) ORGANIZERS: Debargha Banerjee (IISER Pune, India) and Denis Benois (University of Bordeaux, France) DATE: 30 November 2020 to 04 December 2020 VENUE: Online This is a follow up of the conference organized last year arou
From playlist Recent Developments Around P-adic Modular Forms (Online)

BIG Exponents - Modular Exponentiation, Fermat's, Euler's
How to deal with really big exponents using the three main methods: Modular Exponentiation, Fermat's Little Theorem, and Euler's Theorem. Also explains which method to pick. Table of contents: Which to pick? - 0:47 Fermat's Example - 1:39 Modular Exponentiation Example - 4:43 Euler's Exam
From playlist Cryptography and Coding Theory

Resurgence and Partial Theta Series by David Sauzin
Title: Resurgence and Partial Theta Series Speaker: David Sauzin (Institute of Celestial Mechanics and Computation of the Ephemerides, Paris) Date: Friday, 05th August, 2022 Time: 11:00 am (IST) Venue: Hybrid Mode - Offline: Madhava Lecture Hall
From playlist Seminar Series

Jonathan Pila - Multiplicative relations among singular moduli
December 15, 2014 - Analysis, Spectra, and Number theory: A conference in honor of Peter Sarnak on his 61st birthday. I will report on some joint work with Jacob Tsimerman concerning multiplicative relations among singular moduli. Our results rely on the "Ax-Schanuel'' theorem for the j
From playlist Analysis, Spectra, and Number Theory - A Conference in Honor of Peter Sarnak on His 61st Birthday

Introduction To Beilinson--Kato Elements And Their Applications 2 by Chan-Ho Kim
PROGRAM : ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (ONLINE) ORGANIZERS : Ashay Burungale (California Institute of Technology, USA), Haruzo Hida (University of California, Los Angeles, USA), Somnath Jha (IIT - Kanpur, India) and Ye Tian (Chinese Academy of Sciences, China) DA
From playlist Elliptic Curves and the Special Values of L-functions (ONLINE)

Markus Reineke - Cohomological Hall Algebras and Motivic Invariants for Quivers 3/4
We motivate, define and study Donaldson-Thomas invariants and Cohomological Hall algebras associated to quivers, relate them to the geometry of moduli spaces of quiver representations and (in special cases) to Gromov-Witten invariants, and discuss the algebraic structure of Cohomological H
From playlist 2021 IHES Summer School - Enumerative Geometry, Physics and Representation Theory

Rahul Pandharipande - Enumerative Geometry of Curves, Maps, and Sheaves 4/5
The main topics will be the intersection theory of tautological classes on moduli space of curves, the enumeration of stable maps via Gromov-Witten theory, and the enumeration of sheaves via Donaldson-Thomas theory. I will cover a mix of classical and modern results. My goal will be, by th
From playlist 2021 IHES Summer School - Enumerative Geometry, Physics and Representation Theory

Héctor H. Pastén Vásquez: Shimura curves and bounds for the abc conjecture
Abstract: I will explain some new connections between the abc conjecture and modular forms. In particular, I will outline a proof of a new unconditional estimate for the abc conjecture, which lies beyond the existing techniques in this context. The proof involves a number of tools such as
From playlist Algebraic and Complex Geometry

Simplify Exponents Using Product and Quotient
👉 Learn about the rules of exponents. An exponent is a number which a number is raised to, to produce a power. It is the number of times which a number will multiply itself in a power. There are several rules used in evaluating exponents. Some of the rules includes: the product rule, which
From playlist Simplify Using the Rules of Exponents

Haluk SENGUN - Cohomology of arithmetic groups and number theory: geometric, ... 2
In this lecture series, the first part will be dedicated to cohomology of arithmetic groups of lower ranks (e.g., Bianchi groups), their associated geometric models (mainly from hyperbolic geometry) and connexion to number theory. The second part will deal with higher rank groups, mainly
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory
