
Schemes 5: Definition of a scheme
This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne. We give some historical background, then give the definition of a scheme and some simple examples, and finish by explaining the origin of the word "spectrum".
From playlist Algebraic geometry II: Schemes

Olivia Caramello - 2/4 ntroduction to categorical logic, classifying toposes...
Introduction to categorical logic, classifying toposes and the « bridge » technique Construction of classifying toposes for geometric theories. Duality between the subtoposes of the classifying topos of a geometric theory and the quotients of the theory. Transfer of topos‐the
From playlist Topos à l'IHES

Topology 1.7 : More Examples of Topologies
In this video, I introduce important examples of topologies I didn't get the chance to get to. This includes The discrete and trivial topologies, subspace topology, the lower-bound and K topologies on the reals, the dictionary order, and the line with two origins. I also introduce (again)
From playlist Topology

André JOYAL - New variations on the notion of topos
The notion topos is a prominent member of a family of notions which includes that of abelian category, of locally presentable category and of higher topos. We propose two new members: the notion of locus and that of para-topos. The category of pointed spaces and the category of spectra are
From playlist Topos à l'IHES

Olivia Caramello - 3/4 ntroduction to categorical logic, classifying toposes...
Introduction to categorical logic, classifying toposes and the 'bridge' technique Theories classified by a presheaf topos and their quotients. Finite presentability, irreducible formulae and homogeneous models.
From playlist Topos à l'IHES

André JOYAL - 3/4 A crash course in topos theory : the big picture
I will sketch an overall picture of topos theory and of the theory of locales. It includes the notion of sheaf on a site, the notion of forcing topology, of geometric morphism and Giraud's theorem. A useful principle is that a topos is a commutative ring-like object. Every topos is a quoti
From playlist Topos à l'IHES

André JOYAL - 4/4 A crash course in topos theory : the big picture
I will sketch an overall picture of topos theory and of the theory of locales. It includes the notion of sheaf on a site, the notion of forcing topology, of geometric morphism and Giraud's theorem. A useful principle is that a topos is a commutative ring-like object. Every topos is a quoti
From playlist Topos à l'IHES
André JOYAL - 2/4 A crash course in topos theory : the big picture
I will sketch an overall picture of topos theory and of the theory of locales. It includes the notion of sheaf on a site, the notion of forcing topology, of geometric morphism and Giraud's theorem. A useful principle is that a topos is a commutative ring-like object. Every topos is a quoti
From playlist Topos à l'IHES
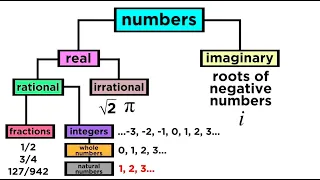
What are the Types of Numbers? Real vs. Imaginary, Rational vs. Irrational
We've mentioned in passing some different ways to classify numbers, like rational, irrational, real, imaginary, integers, fractions, and more. If this is confusing, then take a look at this handy-dandy guide to the taxonomy of numbers! It turns out we can use a hierarchical scheme just lik
From playlist Algebra 1 & 2

Federico Binda - Triangulated Categories of Log Motives over a Field
In this talk I will sketch the construction and highlight the main properties of a new motivic category for logarithmic schemes, log smooth over a ground field k (without log structure). This construction is based on a new Grothendieck topology (called the “dividing topology”) and on the p
From playlist Summer School 2020: Motivic, Equivariant and Non-commutative Homotopy Theory
Étale cohomology lecture 3, August 27, 2020
Sites and sheaves, the étale and fppf site, representable functors
From playlist Étale cohomology and the Weil conjectures

Some directions in derived geometry - Gabriele Vezzosi
Gabriele Vezzosi March 10, 2015 Workshop on Chow groups, motives and derived categories More videos on http://video.ias.edu
From playlist Mathematics

The rising sea: Grothendieck on simplicity and generality - Colin McLarty [2003]
Slides for this talk: https://drive.google.com/file/d/1yDmqhdcKo6-YpDpRdHh2hvuNirZVbcKr/view?usp=sharing Notes for this talk: https://drive.google.com/open?id=1p45B3Hh8WPRhdhQAd0Wq0MvmY0JYSnmc The History of Algebra in the Nineteenth and Twentieth Centuries April 21 - 25, 2003 Colin Mc
From playlist Mathematics

Oliver Röndigs: The slices of Hermitian K-theory (Lecture 1)
The lecture was held within the framework of the (Junior) Hausdorff Trimester Program Topology: Workshop "Hermitian K-theory and trace methods" Abstract: Voevodsky constructed a filtration on the motivic stable homotopy category by measuring how many (de)suspensions with respect to the Ta
From playlist HIM Lectures: Junior Trimester Program "Topology"
Tony Feng - 1/3 Derived Aspects of the Langlands Program
We discuss ways in which derived structures have recently emerged in connection with the Langlands correspondence, with an emphasis on derived Galois deformation rings and derived Hecke algebras. Michael Harris (Columbia Univ.) Tony Feng (MIT)
From playlist 2022 Summer School on the Langlands program

Adam Topaz - The Liquid Tensor Experiment - IPAM at UCLA
Recorded 13 February 2023. Adam Topaz of the University of Alberta presents "The Liquid Tensor Experiment" at IPAM's Machine Assisted Proofs Workshop. Learn more online at: http://www.ipam.ucla.edu/programs/workshops/machine-assisted-proofs/
From playlist 2023 Machine Assisted Proofs Workshop

This lecture is part of an online course on categories. Any object of a category can be thought of as a representable functor in the category of presheaves. We give several examples of representable functors. Then we state Yoneda's lemma, which roughly that morphisms of objects are he sa
From playlist Categories for the idle mathematician

Duality In Higher Categories IV by Pranav Pandit
PROGRAM DUALITIES IN TOPOLOGY AND ALGEBRA (ONLINE) ORGANIZERS: Samik Basu (ISI Kolkata, India), Anita Naolekar (ISI Bangalore, India) and Rekha Santhanam (IIT Mumbai, India) DATE & TIME: 01 February 2021 to 13 February 2021 VENUE: Online Duality phenomena are ubiquitous in mathematics
From playlist Dualities in Topology and Algebra (Online)

Olivia Caramello - 4/4 ntroduction to categorical logic, classifying toposes...
Introduction to categorical logic, classifying toposes and the 'bridge' technique. The ‘bridge-building’ technique: Morita-equivalences as ‘decks’ and site characterizations as ‘arches’. Some examples and applications.
From playlist Topos à l'IHES

A1-algebraic topology : genesis, youth and beyond - Fabien Morel
Vladimir Voevodsky Memorial Conference Topic: A1-algebraic topology : genesis, youth and beyond Speaker: Fabien Morel Affiliation: Mathematisches Instit der Universität München Date: September 11, 2018 For more video please visit http://video.ias.edu
From playlist Vladimir Voevodsky Memorial Conference