
Number theory Full Course [A to Z]
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure #mathematics devoted primarily to the study of the integers and integer-valued functions. Number theorists study prime numbers as well as the properties of objects made out of integers (for example, ratio
From playlist Number Theory

Intro to Number Theory and The Divisibility Relation
This video introduces the divisibility relation and provided several examples. mathispower4u.com
From playlist Additional Topics: Generating Functions and Intro to Number Theory (Discrete Math)

Algebraic number theory and rings I | Math History | NJ Wildberger
In the 19th century, algebraists started to look at extension fields of the rational numbers as new domains for doing arithmetic. In this way the notion of an abstract ring was born, through the more concrete examples of rings of algebraic integers in number fields. Key examples include
From playlist MathHistory: A course in the History of Mathematics

Algebraic number theory and rings II | Math History | NJ Wildberger
In the 19th century, algebraists started to look at extension fields of the rational numbers as new domains for doing arithmetic. In this way the notion of an abstract ring was born, through the more concrete examples of rings of algebraic integers in number fields. Key examples include
From playlist MathHistory: A course in the History of Mathematics

AlgTopReview: An informal introduction to abstract algebra
This is a review lecture on some aspects of abstract algebra useful for algebraic topology. It provides some background on fields, rings and vector spaces for those of you who have not studied these objects before, and perhaps gives an overview for those of you who have. Our treatment is
From playlist Algebraic Topology
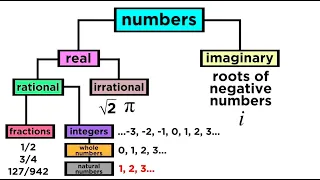
What are the Types of Numbers? Real vs. Imaginary, Rational vs. Irrational
We've mentioned in passing some different ways to classify numbers, like rational, irrational, real, imaginary, integers, fractions, and more. If this is confusing, then take a look at this handy-dandy guide to the taxonomy of numbers! It turns out we can use a hierarchical scheme just lik
From playlist Algebra 1 & 2

In this talk, we will define elliptic curves and, more importantly, we will try to motivate why they are central to modern number theory. Elliptic curves are ubiquitous not only in number theory, but also in algebraic geometry, complex analysis, cryptography, physics, and beyond. They were
From playlist An Introduction to the Arithmetic of Elliptic Curves

Classification of Real Numbers, Inequalities, and Number Line
I define and discuss Real Numbers their subsets of Rational Numbers, Integers, Whole Numbers, Natural Numbers, and finally Irrational Numbers. I finish with Inequalities and the Number line at 23:53 Find free review test, useful notes and more at http://www.mathplane.com If you'd like to
From playlist Algebra 1
Advice to Amateur Research Mathematicians: Poly Number theory-- future directions for greater import
Number theory is a very attractive subject, but in this video we argue that for prospective amateur researchers, the chance of making an important contribution is minimal. Better to focus on a much bigger and more wide open area: Poly Number theory! Polynumbers, developed in the Algebrai
From playlist Maxel inverses and orthogonal polynomials (non-Members)

Basic Algebraic Number Theory - Lecture 1/4 by Liang Xiao [CTNT 2018]
Full playlist: https://www.youtube.com/playlist?list=PLJUSzeW191QxTop6fBSFbSxhzNa376A_c Notes: https://ctnt-summer.math.uconn.edu/wp-content/uploads/sites/1632/2018/05/Xiao-CTNT-notes.pdf Mini-course A: “Basic Algebraic Number Theory” by Liang Xiao (UConn). The goal of this mini-course
From playlist Number Theory

Commutative algebra 1 (Introduction)
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. https://link.springer.com/book/10.1007/978-1-4612-5350-1 This is a short introductory lecture, and gives a few examples of the
From playlist Commutative algebra

A (somewhat) new paradigm for mathematics and physics | Diffusion Symmetry 1 | N J Wildberger
The current understanding of symmetry in mathematics and physics is through group theory. However in the last 120 years, a new strand of thought has gradually appeared in a number of disciplines, from as varied as character theory, strongly regular graphs, von Neumann algebras, Hecke algeb
From playlist Diffusion Symmetry: A bridge between mathematics and physics

A multiset approach to arithmetic | Math Foundations 227 | N J Wildberger
We introduce a new framework for basic arithmetic and algebra, using the data structure of a multiset, or mset. This is an unordered collection of mathematical objects in which repetition is allowed. But what constitutes a "mathematical object"? One way of proceeding is to begin with the s
From playlist Box Arithmetic

On the pioneering works of Professor I.B.S. Passi by Sugandha Maheshwari
PROGRAM GROUP ALGEBRAS, REPRESENTATIONS AND COMPUTATION ORGANIZERS: Gurmeet Kaur Bakshi, Manoj Kumar and Pooja Singla DATE: 14 October 2019 to 23 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Determining explicit algebraic structures of semisimple group algebras is a fund
From playlist Group Algebras, Representations And Computation

This is an experimental video where I give answers to the (mostly) mathematical questions asked by viewers.
From playlist Math talks

An Introduction to Class-S and Tinkertoys (Lecture 2 )by Jacques Distler
Program: Quantum Fields, Geometry and Representation Theory ORGANIZERS : Aswin Balasubramanian, Saurav Bhaumik, Indranil Biswas, Abhijit Gadde, Rajesh Gopakumar and Mahan Mj DATE & TIME : 16 July 2018 to 27 July 2018 VENUE : Madhava Lecture Hall, ICTS, Bangalore The power of symmetries
From playlist Quantum Fields, Geometry and Representation Theory

A brief history of geometry II: The European epoch | Sociology and Pure Mathematics | N J Wildberger
Let's have a quick overview of some of the developments in the European story of geometry -- at least up to the 19th century. We'll discuss Cartesian geometry, Projective geometry, Descriptive geometry, Algebraic geometry and Differential geometry. This is meant for people from outside m
From playlist Sociology and Pure Mathematics

Description of natural, counting, whole, integer, rational and irrational numbers.
From playlist Arithmetic and Pre-Algebra: Number Sense and Properties

Mathematics For Programming | How Much Math Is Needed For Programming For Beginners | Simplilearn
This video on mathematics for programming will give you an idea of how mathematics in programming is helping for the invention of new and creative technologies. The video will also give you an idea about how much math is needed for programming for beginners and make you understand the role
