
Definition of a Field In this video, I define the concept of a field, which is basically any set where you can add, subtract, add, and divide things. Then I show some neat properties that have to be true in fields. Enjoy! What is an Ordered Field: https://youtu.be/6mc5E6x7FMQ Check out
From playlist Real Numbers

Field Definition (expanded) - Abstract Algebra
The field is one of the key objects you will learn about in abstract algebra. Fields generalize the real numbers and complex numbers. They are sets with two operations that come with all the features you could wish for: commutativity, inverses, identities, associativity, and more. They
From playlist Abstract Algebra

Physicists discuss the central role that fields play in modern physics as well as how they use fields in their area of study. This video is part of Perimeter Institute's free educational resource Fields. Download the teacher's guide, modifiable worksheets, and supporting materials at: ht
From playlist Classroom Resources

Worldwide Calculus: Vector Fields
Lecture on 'Vector Fields' from 'Worldwide Multivariable Calculus'. For more lecture videos and $10 digital textbooks, visit www.centerofmath.org.
From playlist Integration and Vector Fields

11_7_1 Potential Function of a Vector Field Part 1
The gradient of a function is a vector. n-Dimensional space can be filled up with countless vectors as values as inserted into a gradient function. This is then referred to as a vector field. Some vector fields have potential functions. In this video we start to look at how to calculat
From playlist Advanced Calculus / Multivariable Calculus

Ordered Fields In this video, I define the notion of an order (or inequality) and then define the concept of an ordered field, and use this to give a definition of R using axioms. Actual Construction of R (with cuts): https://youtu.be/ZWRnZhYv0G0 COOL Construction of R (with sequences)
From playlist Real Numbers

Field Theory: Definition/ Axioms
This video is about the basics axioms of fields.
From playlist Basics: Field Theory

Physics - E&M: Ch 36.1 The Electric Field Understood (1 of 17) What is an Electric Field?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what is an electric field. An electric field exerts a force on a charged place in the field, can be detected by placing a charged in the field and observing the effect on the charge. The stren
From playlist THE "WHAT IS" PLAYLIST

Field Examples - Infinite Fields (Abstract Algebra)
Fields are a key structure in Abstract Algebra. Today we give lots of examples of infinite fields, including the rational numbers, real numbers, complex numbers and more. We also show you how to extend fields using polynomial equations and convergent sequences. Be sure to subscribe so y
From playlist Abstract Algebra

CTNT 2020 - Elliptic curves and the local-global principle for quadratic forms - Asher Auel
The Connecticut Summer School in Number Theory (CTNT) is a summer school in number theory for advanced undergraduate and beginning graduate students, to be followed by a research conference. For more information and resources please visit: https://ctnt-summer.math.uconn.edu/
From playlist CTNT 2020 - Conference Videos

Haowen Zhang - Brauer-Manin and cohomological obstructions to rational points
In the problem of deciding integer or rational solutions of polynomial equations (i.e. finding integer/rational points of a variety), we often first look at the “local” solutions over all the Q_p. When does a collection of local solutions give rise to an honest global solution over Q? Ther
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory

On a Hecke algebra isomorphism of Kazhdan by Radhika Ganapathy
PROGRAM GROUP ALGEBRAS, REPRESENTATIONS AND COMPUTATION ORGANIZERS: Gurmeet Kaur Bakshi, Manoj Kumar and Pooja Singla DATE: 14 October 2019 to 23 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Determining explicit algebraic structures of semisimple group algebras is a fund
From playlist Group Algebras, Representations And Computation

Commutative algebra 61: Examples of regular local rings
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. We give some examples of regular local rings. We first give an example of a regular local ring that is not geometrically regul
From playlist Commutative algebra

Brent Pym: Holomorphic Poisson structures - lecture 2
The notion of a Poisson manifold originated in mathematical physics, where it is used to describe the equations of motion of classical mechanical systems, but it is nowadays connected with many different parts of mathematics. A key feature of any Poisson manifold is that it carries a cano
From playlist Virtual Conference

Alexander Belavin - Spectral Flow Construction of N=2 Superconformal Orbifolds
Ten-dimensional Superstring theory unifies the Standard Model and quantum gravity. To obtain a four-dimensional theory with Space-Time Supersymmetry (which is necessary for phenomenological reasons), as shown by Candelas, Horowitz, Strominger, Witten, we must compactify six of the ten dime
From playlist Mikefest: A conference in honor of Michael Douglas' 60th birthday

Ari Shnidman: Monogenic cubic fields and local obstructions
Recording during the meeting "Zeta Functions" the December 05, 2019 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http:
From playlist Number Theory
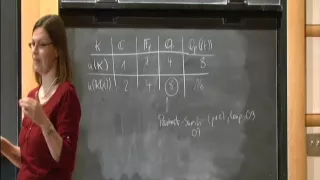
Patching and Local-Global Principles - Julia Hartmann
Julia Hartmann RWTH Aachen University; Member, School of Mathematics November 5, 2012 For more videos, visit http://video.ias.edu
From playlist Mathematics

Local-global compatibility in the crystalline case - Ana Caraiani
Joint IAS/Princeton University Number Theory Seminar Topic: Local-global compatibility in the crystalline case Speaker: Ana Caraiani Affiliation: Imperial College Date: April 16, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics
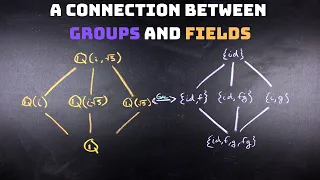
The Structure of Fields: What is a field and a connection between groups and fields
This video is primarily meant to help develop some ideas around the structure of fields and a connection between groups and fields (which will allow me to create more abstract algebra videos in the future! 😀😅🤓) 00:00 Intro 01:04 What is a Field? Here we give the definition of a field in
From playlist The New CHALKboard

Probing electronic properties with Nuclear Magnetic Resonance (Tutorial) by Fabrice Bert
PROGRAM FRUSTRATED METALS AND INSULATORS (HYBRID) ORGANIZERS Federico Becca (University of Trieste, Italy), Subhro Bhattacharjee (ICTS-TIFR, India), Yasir Iqbal (IIT Madras, India), Bella Lake (Helmholtz-Zentrum Berlin für Materialien und Energie, Germany), Yogesh Singh (IISER Mohali, In
From playlist FRUSTRATED METALS AND INSULATORS (HYBRID, 2022)