
Weil conjectures 5: Lefschetz trace formula
This talk explains the relation between the Lefschetz fixed point formula and the Weil conjectures. More precisely, the zeta function of a variety of a finite field can be written in terms of an action of the Frobenius group on the cohomology groups of the variety. The main problem is then
From playlist Algebraic geometry: extra topics

Weil conjectures 1 Introduction
This talk is the first of a series of talks on the Weil conejctures. We recall properties of the Riemann zeta function, and describe how Artin used these to motivate the definition of the zeta function of a curve over a finite field. We then describe Weil's generalization of this to varie
From playlist Algebraic geometry: extra topics
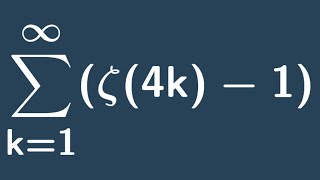
More identities involving the Riemann-Zeta function!
By applying some combinatorial tricks to an identity from https://youtu.be/2W2Ghi9idxM we are able to derive two identities involving the Riemann-Zeta function. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist The Riemann Zeta Function

Some identities involving the Riemann-Zeta function.
After introducing the Riemann-Zeta function we derive a generating function for its values at positive even integers. This generating function is used to prove two sum identities. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist The Riemann Zeta Function

Understanding and computing the Riemann zeta function
In this video I explain Riemann's zeta function and the Riemann hypothesis. I also implement and algorithm to compute the return values - here's the Python script:https://gist.github.com/Nikolaj-K/996dba1ff1045d767b10d4d07b1b032f
From playlist Programming
The Hasse-Weil zeta functions of the intersection cohomology... - YihangZhu
Joint IAS/Princeton University Number Theory Seminar Topic: The Hasse-Weil zeta functions of the intersection cohomology of minimally compactified orthogonal Shimura varieties Speaker: Yihang Zhu Affiliation: Harvard University Date: Oct 20, 2016 For more videos, visit http://video.ias.e
From playlist Mathematics

Semi-Classics, Adiabatic Continuity and Resuregence in Quantum Theories (Lecture 2) by Mithat Unsal
PROGRAM NONPERTURBATIVE AND NUMERICAL APPROACHES TO QUANTUM GRAVITY, STRING THEORY AND HOLOGRAPHY (HYBRID) ORGANIZERS: David Berenstein (University of California, Santa Barbara, USA), Simon Catterall (Syracuse University, USA), Masanori Hanada (University of Surrey, UK), Anosh Joseph (II
From playlist NUMSTRING 2022

Lefschetz fixed point formula, rationality of Weil zeta functions, functional equation
From playlist Étale cohomology and the Weil conjectures

Peter Sarnak, Summation formulae in spectral theory and number theory [2021]
A talk in honor of Zeev Rudnick's 60th birthday Peter Sarnak, Summation formulae in spectral theory and number theory (Institute for Advanced Study and Princeton University) Abstract: The Poisson Summation formula, Riemann-Guinand-Weil explicit formula, Selberg Trace Formula and Lefsche
From playlist Number Theory

Perfect complexes, Lefschetz trace formula with torsion coefficients, intro to the main lemma
From playlist Étale cohomology and the Weil conjectures

Monotonicity of the Riemann zeta function and related functions - P Zvengrowski [2012]
General Mathematics Seminar of the St. Petersburg Division of Steklov Institute of Mathematics, Russian Academy of Sciences May 17, 2012 14:00, St. Petersburg, POMI, room 311 (27 Fontanka) Monotonicity of the Riemann zeta function and related functions P. Zvengrowski University o
From playlist Number Theory

The MAIN LEMMA, Lefschetz pencils, sketch of proof of RH, beginning of proof of Main Lemma
From playlist Étale cohomology and the Weil conjectures

Number Theory 1.1 : Product Formula for the Zeta Function
In this video, I prove Euler's product formula for the Riemann Zeta function. Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : None yet
From playlist Number Theory

Francesc Fité, Sato-Tate groups of abelian varieties of dimension up to 3
VaNTAGe seminar on April 7, 2020 License: CC-BY-NC-SA Closed captions provided by Jun Bo Lau.
From playlist The Sato-Tate conjecture for abelian varieties

Maxim Kontsevich - Resurgence through Path Integrals
I will review the approach to the resurgence phenomenon via integration overrapid decay cycles (Lefschetz thimbles) in path integrals. Examples include WKB asymptotics, heat kernels, WZW models and Chern-Simons theory.
From playlist Resurgence in Mathematics and Physics

Proof of the MAIN LEMMA, cohomology of Lefschetz pencils
From playlist Étale cohomology and the Weil conjectures

Mark Pollicott - Dynamical Zeta functions (Part 2)
Dynamical Zeta functions (Part 1) Licence: CC BY NC-ND 4.0
From playlist École d’été 2013 - Théorie des nombres et dynamique

An Introduction to Tensor Renormalization Group (Lecture 3) by Daisuke Kadoh
PROGRAM NONPERTURBATIVE AND NUMERICAL APPROACHES TO QUANTUM GRAVITY, STRING THEORY AND HOLOGRAPHY (HYBRID) ORGANIZERS: David Berenstein (University of California, Santa Barbara, USA), Simon Catterall (Syracuse University, USA), Masanori Hanada (University of Surrey, UK), Anosh Joseph (II
From playlist NUMSTRING 2022
