
Lefschetz Fixed Point Theorem example
Here we give an example of how to use the Lefschetz fixed point theorem. These notes were really useful as a graduate student, some of them are down now, but I think these notes I had came from here: http://mathsci.kaist.ac.kr/~jinhyun/useful.html
From playlist Riemann Hypothesis
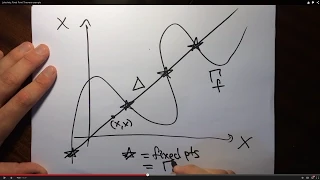
In this video we prove the Lefschetz fixed point theorem assuming some properties of our cohomology theory. These notes were really useful as a graduate student, some of them are down now, but I think these notes I had came from here: http://mathsci.kaist.ac.kr/~jinhyun/useful.html
From playlist Riemann Hypothesis

A beautiful combinatorical proof of the Brouwer Fixed Point Theorem - Via Sperner's Lemma
Using a simple combinatorical argument, we can prove an important theorem in topology without any sophisticated machinery. Brouwer's Fixed Point Theorem: Every continuous mapping f(p) from between closed balls of the same dimension have a fixed point where f(p)=p. Sperner's Lemma: Ever
From playlist Cool Math Series

Paul Shafer:Reverse mathematics of Caristi's fixed point theorem and Ekeland's variational principle
The lecture was held within the framework of the Hausdorff Trimester Program: Types, Sets and Constructions. Abstract: Caristi's fixed point theorem is a fixed point theorem for functions that are controlled by continuous functions but are necessarily continuous themselves. Let a 'Caristi
From playlist Workshop: "Proofs and Computation"

Proof of Lemma and Lagrange's Theorem
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Proof of Lemma and Lagrange's Theorem. This video starts by proving that any two right cosets have the same cardinality. Then we prove Lagrange's Theorem which says that if H is a subgroup of a finite group G then the order of H div
From playlist Abstract Algebra

Weil conjectures 5: Lefschetz trace formula
This talk explains the relation between the Lefschetz fixed point formula and the Weil conjectures. More precisely, the zeta function of a variety of a finite field can be written in terms of an action of the Frobenius group on the cohomology groups of the variety. The main problem is then
From playlist Algebraic geometry: extra topics
Fixed and Periodic Points | Nathan Dalaklis
Fixed Points and Periodic points are two mathematical objects that come up all over the place in Dynamical systems, Differential equations, and surprisingly in Topology as well. In these videos, I introduce the concepts of fixed points and periodic points and gradually build to a proof of
From playlist The New CHALKboard

Visual Group Theory, Lecture 5.4: Fixed points and Cauchy's theorem
Visual Group Theory, Lecture 5.4: Fixed points and Cauchy's theorem We begin with a small lemma stating that if a group of prime order acts on a set S, then the number of fixed points is congruent to the size of the set, modulo p. We need this result to prove Cauchy's theorem, which says
From playlist Visual Group Theory

Karim Alexander Adiprasito - 2/6 - Lefschetz, Hodge and combinatorics...
Lefschetz, Hodge and combinatorics: an account of a fruitful cross-pollination Almost 40 years ago, Stanley noticed that some of the deep theorems of algebraic geometry have powerful combinatorial applications. Among other things, he used the hard Lefschetz theorem to rederive Dynkin's t

Francesc Fité, Sato-Tate groups of abelian varieties of dimension up to 3
VaNTAGe seminar on April 7, 2020 License: CC-BY-NC-SA Closed captions provided by Jun Bo Lau.
From playlist The Sato-Tate conjecture for abelian varieties

Karim Alexander Adiprasito - 1/6 - Lefschetz, Hodge and combinatorics...
Lefschetz, Hodge and combinatorics: an account of a fruitful cross-pollination Almost 40 years ago, Stanley noticed that some of the deep theorems of algebraic geometry have powerful combinatorial applications. Among other things, he used the hard Lefschetz theorem to rederive Dynkin's t

Axioms for the Lefschetz number as a lattice valuation
"Axioms for the Lefschetz number as a lattice valuation" a research talk I gave at the conference on Nielsen Theory and Related Topics in Daejeon Korea, June 28, 2013. Chris Staecker's internet webarea: http://faculty.fairfield.edu/cstaecker/ Nielsen conference webarea: http://open.nims.r
From playlist Research & conference talks

Lefschetz Without Positivity: An Overview - Karim Alexander Adiprasito
Members' Colloquium Topic: Lefschetz Without Positivity: An Overview Speaker: Karim Alexander Adiprasito Affiliation: Hebrew University of Jerusalem, Member, School of Mathematics Date: February 6, 2023 2:00pm|Simonyi Hall 101 and Remote Access - see Zoom link below The Lefschetz propert
From playlist Mathematics

Karim Alexander Adiprasito - 4/6 - Lefschetz, Hodge and combinatorics...
Lefschetz, Hodge and combinatorics: an account of a fruitful cross-pollination Almost 40 years ago, Stanley noticed that some of the deep theorems of algebraic geometry have powerful combinatorial applications. Among other things, he used the hard Lefschetz theorem to rederive Dynkin's t

Karim Alexander Adiprasito - 3/6 - Lefschetz, Hodge and combinatorics...
Lefschetz, Hodge and combinatorics: an account of a fruitful cross-pollination Almost 40 years ago, Stanley noticed that some of the deep theorems of algebraic geometry have powerful combinatorial applications. Among other things, he used the hard Lefschetz theorem to rederive Dynkin's t

Mark Hughes: Branched Coverings Over Surface Braids and (Broken) Lefschetz Fibrations
Mark Hughes, Brigham Young University Title: Branched Coverings Over Surface Braids and (Broken) Lefschetz Fibrations on Non- compact 4-Manifold In this talk I will discuss a construction of Lefschetz type fibrations on 4–manifolds via coverings branched over braided surfaces. When applied
From playlist 39th Annual Geometric Topology Workshop (Online), June 6-8, 2022

Karim Alexander Adiprasito - 5/6 - Lefschetz, Hodge and combinatorics...
Lefschetz, Hodge and combinatorics: an account of a fruitful cross-pollination Almost 40 years ago, Stanley noticed that some of the deep theorems of algebraic geometry have powerful combinatorial applications. Among other things, he used the hard Lefschetz theorem to rederive Dynkin's t
