
How To Construct An Isosceles Triangle
Complete videos list: http://mathispower4u.yolasite.com/ This video will show how to construct an isosceles triangle with a compass and straight edge.
From playlist Triangles and Congruence

Determine if a set of points is a parallelogram by using the slope formula
👉 Learn how to determine the figure given four points. A quadrilateral is a polygon with four sides. Some of the types of quadrilaterals are: parallelogram, square, rectangle, rhombus, kite, trapezoid, etc. Each of the types of quadrilateral has its properties. Given four points that repr
From playlist Quadrilaterals on a Coordinate Plane

👉 Learn the essential definitions of triangles. A triangle is a polygon with three sides. Triangles are classified on the basis of their angles or on the basis of their side lengths. The classification of triangles on the bases of their angles are: acute, right and obtuse triangles. The cl
From playlist Types of Triangles and Their Properties
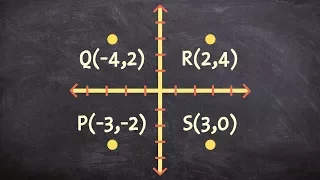
Using the slope formula to determine if points make up a rectangle
👉 Learn how to determine the figure given four points. A quadrilateral is a polygon with four sides. Some of the types of quadrilaterals are: parallelogram, square, rectangle, rhombus, kite, trapezoid, etc. Each of the types of quadrilateral has its properties. Given four points that repr
From playlist Quadrilaterals on a Coordinate Plane

Determine if a set of points makes up a rectangle using the distance formula
👉 Learn how to determine the figure given four points. A quadrilateral is a polygon with four sides. Some of the types of quadrilaterals are: parallelogram, square, rectangle, rhombus, kite, trapezoid, etc. Each of the types of quadrilateral has its properties. Given four points that repr
From playlist Quadrilaterals on a Coordinate Plane
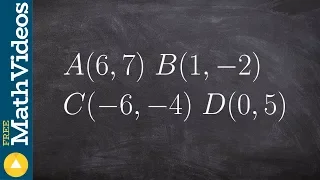
Determining if a set of points makes a parallelogram or not
👉 Learn how to determine the figure given four points. A quadrilateral is a polygon with four sides. Some of the types of quadrilaterals are: parallelogram, square, rectangle, rhombus, kite, trapezoid, etc. Each of the types of quadrilateral has its properties. Given four points that repr
From playlist Quadrilaterals on a Coordinate Plane

Using a set of points determine if the figure is a parallelogram using the midpoint formula
👉 Learn how to determine the figure given four points. A quadrilateral is a polygon with four sides. Some of the types of quadrilaterals are: parallelogram, square, rectangle, rhombus, kite, trapezoid, etc. Each of the types of quadrilateral has its properties. Given four points that repr
From playlist Quadrilaterals on a Coordinate Plane

CTNT 2020 - Elliptic curves and the local-global principle for quadratic forms - Asher Auel
The Connecticut Summer School in Number Theory (CTNT) is a summer school in number theory for advanced undergraduate and beginning graduate students, to be followed by a research conference. For more information and resources please visit: https://ctnt-summer.math.uconn.edu/
From playlist CTNT 2020 - Conference Videos
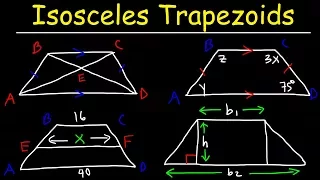
This geometry video tutorial provides a basic introduction into isosceles trapezoids. It discusses the basic properties of isosceles trapezoids. The bases are parallel and the legs are congruent. The lower base angles are congruent and the upper base angles are congruent. The lower bas
From playlist Geometry Video Playlist

Determine if a set of points is a parallelogram using the distance formula
👉 Learn how to determine the figure given four points. A quadrilateral is a polygon with four sides. Some of the types of quadrilaterals are: parallelogram, square, rectangle, rhombus, kite, trapezoid, etc. Each of the types of quadrilateral has its properties. Given four points that repr
From playlist Quadrilaterals on a Coordinate Plane

Milnor Conjecture Learning Seminar - Akshay Venkatesh
February 24, 2023 1:00pm – 3:30pm Rubenstein Commons Meeting Room 5 Speaker: Akshay Venkatesh
From playlist Milnor Conjecture Learning Seminar
Patching and Local-Global Principles - Julia Hartmann
Julia Hartmann RWTH Aachen University; Member, School of Mathematics November 5, 2012 For more videos, visit http://video.ias.edu
From playlist Mathematics

Yonatan Harpaz - New perspectives in hermitian K-theory II
Warning: around 32:30 in the video, in the slide entitled "Karoubi's conjecture", a small mistake was made - in the third bulleted item the genuine quadratic structure appearing should be the genuine symmetric one (so both the green and red instances of the superscript gq should be gs), an
From playlist New perspectives on K- and L-theory

Jacques Tits: Algebraic simple groups and buildings
This lecture was held by Abel Laureate Jacques Tits at The University of Oslo, May 21, 2008 and was part of the Abel Prize Lectures in connection with the Abel Prize Week celebrations. Program for the Abel Lectures 2008 1. Abel Laureate John Thompson: “Dirichlet series and SL(2,Z)" 2
From playlist Abel Lectures

Ben Howard: Supersingular points on som orthogonal and unitary Shimura varieties
To an orthogonal group of signature (n,2), or to a unitary group of any signature, one can attach a Shimura variety. The general problem is to describe the integral models of these Shimura varieties, and their reductions modulo various primes. I will give a conjectural description of the s
From playlist HIM Lectures: Junior Trimester Program "Algebraic Geometry"

Algorithms for motion of networks by weighted mean curvature – Selim Esedoğlu – ICM2018
Mathematics in Science and Technology Invited Lecture 17.13 Algorithms for motion of networks by weighted mean curvature Selim Esedoğlu Abstract: I will report on recent developments in a class of algorithms, known as threshold dynamics, for computing the motion of interfaces by mean cur
From playlist Mathematics in Science and Technology

Retract rationality of some (exceptional) group varieties by Maneesh Thakur
DATE & TIME 05 November 2016 to 14 November 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore Computational techniques are of great help in dealing with substantial, otherwise intractable examples, possibly leading to further structural insights and the detection of patterns in many abstra
From playlist Group Theory and Computational Methods

Milnor Conjecture Learning Seminar - 2023-03-17
From playlist Mathematics

Arithmetic theta series - Stephan Kudla
Workshop on Representation Theory and Analysis on Locally Symmetric Spaces Topic: Arithmetic theta series Speaker: Stephan Kudla Affiliation: University of Toronto Date: March 8, 2018 For more videos, please visit http://video.ias.edu
From playlist Mathematics
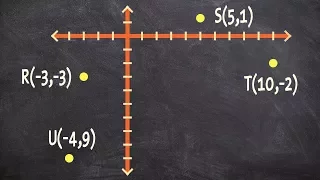
Determine if a set of points is a trapezoid or not
👉 Learn how to determine the figure given four points. A quadrilateral is a polygon with four sides. Some of the types of quadrilaterals are: parallelogram, square, rectangle, rhombus, kite, trapezoid, etc. Each of the types of quadrilateral has its properties. Given four points that repr
From playlist Quadrilaterals on a Coordinate Plane