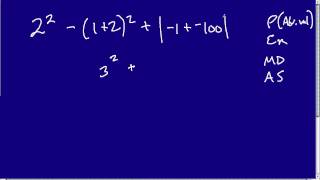
A short description of absolute value
From playlist Arithmetic and Pre-Algebra: Negative Numbers

Math 101 091117 Introduction to Analysis 05 Absolute Value
Absolute value: definition. Notion of distance. Properties of the absolute value: proofs. Triangle inequality
From playlist Course 6: Introduction to Analysis (Fall 2017)

What is the definition of absolute value
http://www.freemathvideos.com In this video playlist you will learn how to solve and graph absolute value equations and inequalities. When working with absolute value equations and functions it is important to understand that the absolute value symbol represents the absolute distance from
From playlist Solve Absolute Value Equations

Absolute Value Inequality Algebra 2
In this problem, we solve an absolute value inequality.
From playlist Algebra 2 Chapter 1 Take Home Test

Using parent graphs to understand the left and right hand limits
👉 Learn how to evaluate the limit of an absolute value function. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The absolute value function is a function which only takes the positive val
From playlist Evaluate Limits of Absolute Value

Sum of Absolute Values: solve an inequality
#mathonshorts #shorts The geometric interpretation of the absolute value is important in solving this problem. On a real number line, |x-a| is the distance between a real number x and a constant a.
From playlist "Smarter In-A-Minute" Math on Shorts

Absolute Value and Algebraic Expressions
a worked example dealing with absolute value and algebra
From playlist Pre Calc

Absolute versus relative measurements in geometry | Rational Geometry Math Foundations 134
In science and ordinary life, the distinction between absolute and relative measurements is very useful. It turns out that in mathematics this is also an important distinction. We must be prepared that some aspects of mathematics are more naturally measured relatively, rather than absolute
From playlist Math Foundations

R. Perales - Recent Intrinsic Flat Convergence Theorems
Given a closed and oriented manifold M and Riemannian tensors g0, g1, ... on M that satisfy g0 gj, vol(M, gj)→vol (M, g0) and diam(M, gj)≤D we will see that (M, gj) converges to (M, g0) in the intrinsic flat sense. We also generalize this to the non-empty bundary setting. We remark that u
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

R. Perales - Recent Intrinsic Flat Convergence Theorems (version temporaire)
Given a closed and oriented manifold M and Riemannian tensors g0, g1, ... on M that satisfy g0 gj, vol(M, gj)→vol (M, g0) and diam(M, gj)≤D we will see that (M, gj) converges to (M, g0) in the intrinsic flat sense. We also generalize this to the non-empty bundary setting. We remark that u
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

Christina Sormani: A Course on Intrinsic Flat Convergence part 1
Intrinsic Flat Convergence was first introduced in joint work with Stefan Wenger building upon work of Ambrosio-Kirchheim to address a question proposed by Tom Ilmanen. In this talk, I will present an overview of the initial paper on the topic [JDG 2011]. I will briefly describe key examp
From playlist HIM Lectures 2015

Christina Sormani - Sequences of manifolds with lower bounds on their scalar curvature
If one has a weakly converging sequence of manifolds with a uniform lower bound on their scalar curvature, what properties of scalar curvature persist on the limit space? What additional hypotheses might be added to provide stronger controls on the limit space? What hypotheses are requ
From playlist Not Only Scalar Curvature Seminar

C. Sormani - Intrinsic Flat and Gromov-Hausdorff Convergence 4 (version temporaire)
We introduce various notions of convergence of Riemannian manifolds and metric spaces. We then survey results and open questions concerning the limits of sequences of Riemannian manifolds with uniform lower bounds on their scalar curvature. We close the course by presenting methods and the
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

C. Sormani - Intrinsic Flat and Gromov-Hausdorff Convergence 1
We introduce various notions of convergence of Riemannian manifolds and metric spaces. We then survey results and open questions concerning the limits of sequences of Riemannian manifolds with uniform lower bounds on their scalar curvature. We close the course by presenting methods and the
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

C. Sormani - Intrinsic Flat and Gromov-Hausdorff Convergence 1 (version temporaire)
We introduce various notions of convergence of Riemannian manifolds and metric spaces. We then survey results and open questions concerning the limits of sequences of Riemannian manifolds with uniform lower bounds on their scalar curvature. We close the course by presenting methods and the
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

C. Sormani - Intrinsic Flat and Gromov-Hausdorff Convergence 4
We introduce various notions of convergence of Riemannian manifolds and metric spaces. We then survey results and open questions concerning the limits of sequences of Riemannian manifolds with uniform lower bounds on their scalar curvature. We close the course by presenting methods and the
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

Christina Sormani - Currents on metric spaces and intrinsic flat convergence
First I will provide a brief introduction to Ambrosio-Kirchheim’s Theory of Currents on Metric Spaces. Then I will review joint work with Wenger defining integral current spaces and intrinsic flat convergence. This will provide sufficient background needed to follow the talk of Antoine Son
From playlist Not Only Scalar Curvature Seminar

Stability of the spacetime positive mass theorem in spherical symmetry - Marcus Khuri
More videos on http://video.ias.edu
From playlist Mathematics

CCSS What is the difference between Acute, Obtuse, Right and Straight Angles
👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships
