
11_7_1 Potential Function of a Vector Field Part 1
The gradient of a function is a vector. n-Dimensional space can be filled up with countless vectors as values as inserted into a gradient function. This is then referred to as a vector field. Some vector fields have potential functions. In this video we start to look at how to calculat
From playlist Advanced Calculus / Multivariable Calculus
Find the Gradient Vector Field of f(x,y)=x^3y^5
This video explains how to find the gradient of a function. It also explains what the gradient tells us about the function. The gradient is also shown graphically. http://mathispower4u.com
From playlist The Chain Rule and Directional Derivatives, and the Gradient of Functions of Two Variables
One prominent example of a vector field is the Gradient Vector Field. Given any scalar, multivariable function f: R^n\to R, we can get a corresponding vector field that has a precise geometrical meaning: the vectors point in the direction of maximal increase of the function. MY VECTOR CA

Find the Gradient Vector Field of f(x,y)=ln(2x+5y)
This video explains how to find the gradient of a function. It also explains what the gradient tells us about the function. The gradient is also shown graphically. http://mathispower4u.com
From playlist The Chain Rule and Directional Derivatives, and the Gradient of Functions of Two Variables

Conservative vector fields | Lecture 44 | Vector Calculus for Engineers
The definition of a conservative vector field, and an example of how to find a potential function. Join me on Coursera: https://www.coursera.org/learn/vector-calculus-engineers Lecture notes at http://www.math.ust.hk/~machas/vector-calculus-for-engineers.pdf Subscribe to my channel: h
From playlist Vector Calculus for Engineers

Introduction to Vector Fields This video discusses, 1) The definition of a vector field. 2) Examples of vector fields including the gradient, and various velocity fields. 3) The definition of a conservative vector field. 4) The definition of a potential function. 5) Test for conservative
From playlist Calculus 3

Physics - Advanced E&M: Ch 1 Math Concepts (10 of 55) What is the Gradient of a Scalar?
Visit http://ilectureonline.com for more math and science lectures! In this video I will develop the equation of the gradient of a scalar in 2-D space. Next video in this series can be seen at: https://youtu.be/rZ2AQpcWHzw
From playlist PHYSICS 67 ADVANCED ELECTRICITY & MAGNETISM

Download the free PDF http://tinyurl.com/EngMathYT A basic tutorial on the gradient field of a function. We show how to compute the gradient; its geometric significance; and how it is used when computing the directional derivative. The gradient is a basic property of vector calculus. NOT
From playlist Engineering Mathematics

What Does the Gradient Vector Mean Intuitively?
What Does the Gradient Vector Mean Intuitively? If you enjoyed this video please consider liking, sharing, and subscribing. You can also help support my channel by becoming a member https://www.youtube.com/channel/UCr7lmzIk63PZnBw3bezl-Mg/join Thank you:)
From playlist Calculus 3

Are all vector fields the gradient of a potential? ... and the Helmholtz Decomposition
This video asks a classic question: are all vector fields the gradient of a potential field? The answer is no, but by understanding why, we prepare ourselves for potential flows in the next videos. @eigensteve on Twitter eigensteve.com databookuw.com %%% CHAPTERS %%% 0:00 Introducti
From playlist Engineering Math: Vector Calculus and Partial Differential Equations

Worldwide Calculus: Vector Fields
Lecture on 'Vector Fields' from 'Worldwide Multivariable Calculus'. For more lecture videos and $10 digital textbooks, visit www.centerofmath.org.
From playlist Integration and Vector Fields

Worldwide Calculus: Conservative Vector Fields
Lecture on 'Conservative Vector Fields' from 'Worldwide Multivariable Calculus'. For more lecture videos and $10 digital textbooks, visit www.centerofmath.org.
From playlist Integration and Vector Fields

Calculus 3 Lecture 15.1: INTRODUCTION to Vector Fields (and what makes them Conservative)
Calculus 3 Lecture 15.1: INTRODUCTION to Vector Fields (and what makes them Conservative): What Vector Fields are, and what they look like. We discuss graphing Vector Fields in 2-D and 3-D and talk about what a Conservative Vector Field means.
From playlist Calculus 3 (Full Length Videos)

ME564 Lecture 22: Div, Grad, and Curl
ME564 Lecture 22 Engineering Mathematics at the University of Washington Div, Grad, and Curl Notes: http://faculty.washington.edu/sbrunton/me564/pdf/L22.pdf Course Website: http://faculty.washington.edu/sbrunton/me564/ http://faculty.washington.edu/sbrunton/
From playlist Engineering Mathematics (UW ME564 and ME565)

MATH2018 Lecture 2.3 Gradient and Directional Derivative
We introduce the concepts of the gradient and directional derivative, which tell us how a scalar field varies in space.
From playlist MATH2018 Engineering Mathematics 2D

MATH2018 Lecture 2.4 Level Surfaces, Tangent Planes, and Normal Lines
We discuss how the gradient of a scalar field is related to the concept of a level surface, and show how we can use it to define the tangent plane and normal line at a point.
From playlist MATH2018 Engineering Mathematics 2D

Math 032 Multivariable Calculus 18 110714: Vector Fields; Line Integrals
Vector fields; gradient fields; potential function; conservation of energy; line integrals of functions with respect to arc length
From playlist Course 4: Multivariable Calculus (Fall 2014)

Fundamental theorem of line integrals. Chris Tisdell UNSW
This lecture discusses the "fundamental theorem of line integrals for gradient fields". The topic is motivated and the theorem is stated and proved. A number of examples are presented to illustrate the theory.
From playlist Vector Calculus @ UNSW Sydney. Dr Chris Tisdell

19: Vector Fields - Valuable Vector Calculus
Visualizing and graphing vector fields to understand vector-valued functions. The gradient is an example! Full Valuable Vector Calculus playlist: https://www.youtube.com/playlist?list=PLug5ZIRrShJHgsWPng59fFFoqn183aO-1 New math videos every Monday and Friday. Subscribe to make sure you s
From playlist Valuable Vector Calculus

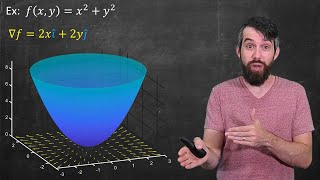
The Gradient Operator in Vector Calculus: Directions of Fastest Change & the Directional Derivative
This video introduces the gradient operator from vector calculus, which takes a scalar field (like the temperature distribution in a room) and returns a vector field with the direction of fastest change in the temperature at every point. The gradient is a fundamental building block in vec
From playlist Engineering Math: Vector Calculus and Partial Differential Equations