
Corinne Blondel - Godement le professeur, Godement l'objecteur
Godement le mathématicien était un enseignant hors pair, transmettant sa passion pour les mathématiques dans toute son exigence sans jamais omettre de rappeler la responsabilité morale du scientifique. Son Cours d'Algèbre est emblématique de cette démarche, ainsi que les volumes d'Analyse
From playlist Reductive groups and automorphic forms. Dedicated to the French school of automorphic forms and in memory of Roger Godement.

Jean Pierre Labesse - L’héritage de Roger Godement
J’évoquerai tout d’abord la carrière scientifique de Roger Godement, ses goûts et son influence via ses exposés, ses cours et ses élèves. Dans une seconde partie j’exposerai l’état du travail avec Bertrand Lemaire sur la formule des traces en caractéristique positive. Ce se
From playlist Reductive groups and automorphic forms. Dedicated to the French school of automorphic forms and in memory of Roger Godement.

Peter Schneider - Progress report on derived Hecke
In the modular smooth representation theory of p-adic reductive groups with coefficents in a field of characteristic p (same p!) a close relation between smooth representations and modules over suitable Hecke algebras only holds in a derived version. This leads to differenti
From playlist Reductive groups and automorphic forms. Dedicated to the French school of automorphic forms and in memory of Roger Godement.

Hervé Jacquet - The work of Roger Godement
I will discuss the work of Roger Godement. I will present the part of his work which is not accessible to the general public because it consists of letters or private notes. I will try to stress the influence of Godement on the theory of automorphic representations.
From playlist Reductive groups and automorphic forms. Dedicated to the French school of automorphic forms and in memory of Roger Godement.

Programming Terms: Idempotence
In this programming terms video, we will be going over Idempotence. Idempotence is the property of certain operations in mathematics and computer science, that can be applied multiple times without changing the result beyond the initial application. Let's take a look at this definition in-
From playlist Programming Terms

Bergeron Nicolas "Les "invariants arithmétiques" de H. Poincaré"
Note(s) Biographique(s) Nicolas Bergeron est né en 1975. Elève de l'ENS Lyon il obtiendra son doctorat en 2000. Lauréat de la Médaille de bronze du C.N.R.S. en 2007, il a également été membre junior de l'IUF en 2010. Il est actuellement professeur de mathématiques à l'Université Pierre
From playlist Colloque Scientifique International Poincaré 100

Simplifying an expression with a parenthesis ex 4, 10 - (2^3 + 4)/3 - 1
👉 Learn how to simplify mathematics expressions. A mathematis expression is a finite combination of numbers and symbols formed following a set of operations or rules. To simplify a mathematics expression means to reduce the expression into simpler form. For expressions having parenthesis
From playlist Simplify Expressions Using Order of Operations
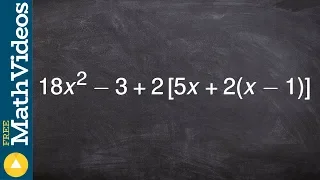
How to simplify an expression by following order of operations and distributive property
👉 Learn how to simplify mathematics expressions. A mathematis expression is a finite combination of numbers and symbols formed following a set of operations or rules. To simplify a mathematics expression means to reduce the expression into simpler form. For expressions having parenthesis
From playlist Simplify Expressions Using Order of Operations
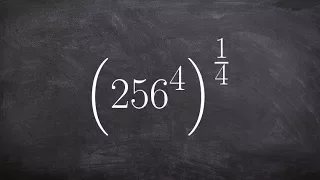
Applying the power rule to simplify an expression with a rational power
👉 Learn how to simplify rational powers using the power rule. There are some laws of exponents which might come handy when simplifying expressions with exponents. Some of the laws include the power rule which states that when an expression with an exponent is raised to another exponent tha
From playlist Raise an Exponent to a Fraction

Wen Wei Li - Sur la stabilisation de la formule des traces...
Wen Wei Li - Sur la stabilisation de la formule des traces pour c ertains revêtements des groupes symplectiques La stabilisation de la formule des traces pour les revêtements est largement inconnu, à l'exception notable du revêtement à deux feuillets de Sp(2n), qui utilise la représentat
From playlist Reductive groups and automorphic forms. Dedicated to the French school of automorphic forms and in memory of Roger Godement.

Ramla Abdellatif - Iwahori - Hecke algebras and hovels for split Kac - Moody groups
Let F be a non-archimedean local field and G be the group of F-rational points of a connected reductive group defined over F. The study of (complex smooth) representations of G imply various tools coming from different nature. These include in particular induction functors, Hecke al
From playlist Reductive groups and automorphic forms. Dedicated to the French school of automorphic forms and in memory of Roger Godement.

Use the Division Algorithm to Find the Remainder and Quotient when Dividing Integers
Use the Division Algorithm to Find the Remainder and Quotient when Dividing Integers If you enjoyed this video please consider liking, sharing, and subscribing. Udemy Courses Via My Website: https://mathsorcerer.com My FaceBook Page: https://www.facebook.com/themathsorcerer There are s
From playlist Divisibility and Primes
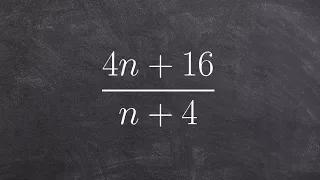
Simplifying rational expression
Learn how to simplify rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To simplify a rational expression, we factor completely the numerator and the denominator of the rational
From playlist Simplify Rational Expressions (Binomials) #Rational

On the kernel of the non abelian Fourier transform - Ngo Bao Chau
Joint IAS/PU Number Theory Seminar Topic: On the kernel of the non abelian Fourier transform Speaker: Ngo Bao Chau Affiliation: University of Chicago Date: October 20, 2022 Tate reformulated the theory of the Riemann zeta function and its functional equation as the Mellin shadow of the F
From playlist Mathematics

Simplifying an expression with four operations- Online Math Tutor-Simplify
👉 Learn how to simplify mathematics expressions. A mathematis expression is a finite combination of numbers and symbols formed following a set of operations or rules. To simplify a mathematics expression means to reduce the expression into simpler form. For expressions having parenthesis
From playlist Simplify Expressions Using Order of Operations

Simplify an expression by applying distributive property across parenthesis and brackets
👉 Learn how to simplify mathematics expressions. A mathematis expression is a finite combination of numbers and symbols formed following a set of operations or rules. To simplify a mathematics expression means to reduce the expression into simpler form. For expressions having parenthesis
From playlist Simplify Expressions Using Order of Operations
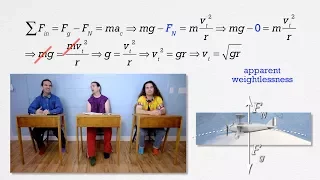
Number of g's or g-Forces Introduction
Description and examples of g-forces or number of g’s. Want Lecture Notes? http://www.flippingphysics.com/g-forces.html This is an AP Physics 1 topic. 0:00 Intro 0:14 Equations for g-forces or number of g’s 1:08 Number of g’s when at rest on the surface of the Earth 2:43 Number of g’s whe
From playlist Gravity - A Level Physics

Vincent Sécherre - Congruence properties of endoclasses...
Congruence properties of endoclasses and the local Jacquet-Langlands correspondence Consider the local Jacquet-Langlands correspondence between the discrete series representations of a general linear group H over some non-Archimedean locally compact field F and those of an inner form G of
From playlist Reductive groups and automorphic forms. Dedicated to the French school of automorphic forms and in memory of Roger Godement.

Eric Urban - Relations entières de périodes pour le changement de base
L’étude des congruences entre un changement de base d’une forme modulaire elliptique à une extension quadratique F/Q avec des formes qui n’en sont pas est étroitement liée aux relations entières entre les périodes du changement de base et celles de la forme de
From playlist Reductive groups and automorphic forms. Dedicated to the French school of automorphic forms and in memory of Roger Godement.

Simplify an expression using power to product and power to quotient rule
👉 Learn how to simplify expressions using the power rule of exponents. When several terms of an expression is raised to an exponent outside the parenthesis, the exponent is distributed over the individual terms in the expression and the exponent outside the parenthesis is multiplied to eac
From playlist Simplify Using the Rules of Exponents