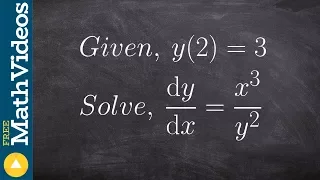
How to find the particular solution of a differential equation
Learn how to solve the particular solution of differential equations. A differential equation is an equation that relates a function with its derivatives. The solution to a differential equation involves two parts: the general solution and the particular solution. The general solution give
From playlist Solve Differential Equation (Particular Solution) #Integration

How to determine the general solution to a differential equation
Learn how to solve the particular solution of differential equations. A differential equation is an equation that relates a function with its derivatives. The solution to a differential equation involves two parts: the general solution and the particular solution. The general solution give
From playlist Differential Equations

(3.2.4A) Solving a System of Linear Equations Using an Augmented Matrix
This lesson explains how to solve a system of equations using an augmented matrix. https://mathispower4u.com
From playlist Differential Equations: Complete Set of Course Videos

Find the particular solution given the conditions and second derivative
Learn how to solve the particular solution of differential equations. A differential equation is an equation that relates a function with its derivatives. The solution to a differential equation involves two parts: the general solution and the particular solution. The general solution give
From playlist Solve Differential Equation (Particular Solution) #Integration

How to solve a separable differential equation
Learn how to solve the particular solution of differential equations. A differential equation is an equation that relates a function with its derivatives. The solution to a differential equation involves two parts: the general solution and the particular solution. The general solution give
From playlist Solve Differential Equation (Particular Solution) #Integration

Differential Equations | First Order Linear System of DEs.
We solve a nonhomogeneous system of first order linear differential equations using a strategy inspired from solving a single first order linear differential equation. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Systems of Differential Equations

Differential Equations | Exact Equations and Integrating Factors Example 2
We give an example of converting a non-exact differential equation into an exact equation. We use this to solve the differential equation.
From playlist Numerical Methods for Differential Equations

How to solve a differentialble equation by separating the variables
Learn how to solve the particular solution of differential equations. A differential equation is an equation that relates a function with its derivatives. The solution to a differential equation involves two parts: the general solution and the particular solution. The general solution give
From playlist Solve Differential Equation (Particular Solution) #Integration

Giuseppe Mingione - 23 September 2016
Mingione, Giuseppe "Recent progresses in nonlinear potential theory"
From playlist A Mathematical Tribute to Ennio De Giorgi

Introduction to Differential Equations
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Introduction to Differential Equations - The types of differential equations, ordinary versus partial. - How to find the order of a differential equation.
From playlist Differential Equations

Jérémie Szeftel The resolution of the bounded L2 curvature conjecture in General Relativity (Part 1)
In order to control locally a space-time which satisfies the Einstein equations, what are the minimal assumptions one should make on its curvature tensor? The bounded L2 curvature conjecture roughly asserts that one should only need L2 bounds of the curvature tensor on a given space-like
From playlist Ecole d'été 2014 - Analyse asymptotique en relativité générale

Igor Rodnianski - Contributions of Sergiu Klainerman to hyperbolic PDE's and General Relativity
Princeton University - January 26, 2016 This talk was part of "Analysis, PDE's, and Geometry: A conference in honor of Sergiu Klainerman"
From playlist Anlaysis, PDE's, and Geometry: A conference in honor of Sergiu Klainerman

[BOURBAKI 2019]Estimations pseudo-spectrales et stabilité des tourbillons plans - Gallay -16/10/2019
Gallay () / 16.11.2019 Estimations pseudo-spectrales et stabilité des tourbillons plans Lorsqu'on étudie la stabilité des écoulements parallèles ou tourbillonnaires en mécanique des fluides, on observe que les effets de transport renforcent considérablement la dissipation visqueuse. C
From playlist BOURBAKI - 2019

Lecture Lorenzo Pareschi: Uncertainty quantification for kinetic equations III
The lecture was held within the of the Hausdorff Trimester Program: Kinetic Theory Abstract: In these lectures we overview some recent results in the field of uncertainty quantification for kinetic equations with random inputs. Uncertainties may be due to various reasons, like lack of kn
From playlist Summer School: Trails in kinetic theory: foundational aspects and numerical methods

Maximum Likelihood Estimation (MLE) | Score equation | Information | Invariance
For all videos see http://www.zstatistics.com/ 0:00 Introduction 2:50 Definition of MLE 4:59 EXAMPLE 1 (visually identifying MLE from Log-likelihood plot) 10:47 Score equation 12:15 Information 14:31 EXAMPLE 1 calculations (finding the MLE and creating a confidence interval) 19:21 Propert
From playlist Statistical Inference (7 videos)

19/11/2015 - Gustav Holzegel - The Linear Stability of the Schwarzschild Solution
The Linear Stability of the Schwarzschild Solution Under Gravitational Perturbations https://philippelefloch.files.wordpress.com/2015/11/2015-ihp-g-holzegel.pdf
From playlist 2015-T3 - Mathematical general relativity - CEB Trimester

Alexandre Sukhov - J-complex curves: some applications (Part 3)
We will focus in our lectures on the following : 1. J-complex discs in almost complex manifolds : general properties. Linearization and compactness. Gromov’s method : the Fredholm alternative for the d-bar operator. Attaching a complex disc to a Lagrangian manifold. Application : exotic sy
From playlist École d’été 2012 - Feuilletages, Courbes pseudoholomorphes, Applications

Hajar Bahouri - De l'analyse des EDPs non linéaires à la théorie des groupes
Créteil, Prix Paul Doisteau 2016 Réalisation technique : Antoine Orlandi (GRICAD) | Tous droits réservés
From playlist Des mathématiciens primés par l'Académie des Sciences 2017

Introduction to Homogeneous Differential Equations
Introduction to Homogeneous Differential Equations A full introduction to homogeneous differential equations.
From playlist Differential Equations