
Towards Strong Minimality and the Fuchsian Triangle Groups - J. Nagloo - Workshop 3 - CEB T1 2018
Joel Nagloo (City University of New York) / 29.03.2018 Towards Strong Minimality and the Fuchsian Triangle Groups From the work of Freitag and Scanlon, we have that the ODEs satisfied by the Hauptmoduls of arithmetic subgroups of SL2(Z) are strongly minimal and geometrically trivial. A c
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields

Alan Reid: Distinguishing certain triangle groups by their finite quotients
The lecture was held within the framework of the Hausdorff Trimester Program: Logic and Algorithms in Group Theory. Abstract: We prove that certain arithmetic Fuchsian triangle groups are profinitely rigid in the sense that they are determined by their set of finite quotients amongst all
From playlist HIM Lectures: Trimester Program "Logic and Algorithms in Group Theory"

Michael Wibmer: Etale difference algebraic groups
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebraic and Complex Geometry

Definition of a group Lesson 24
In this video we take our first look at the definition of a group. It is basically a set of elements and the operation defined on them. If this set of elements and the operation defined on them obey the properties of closure and associativity, and if one of the elements is the identity el
From playlist Abstract algebra

Group theory 20: Frobenius groups
This lecture is part of an online mathematics course on group theory. It gives several examples of Frobenius groups (permutation groups where any element fixing two points is the identity).
From playlist Group theory

Symmetric Groups (Abstract Algebra)
Symmetric groups are some of the most essential types of finite groups. A symmetric group is the group of permutations on a set. The group of permutations on a set of n-elements is denoted S_n. Symmetric groups capture the history of abstract algebra, provide a wide range of examples in
From playlist Abstract Algebra

Strong minimality for Painleve equations and Fuchsian equations Strong minimality is a central notion in model theory which has an interpretation in differential algebra as a functional transcendence statement. We will talk about some new proofs of strong minimality for differential equat
From playlist DART X

Mima Stanojkovski - Groups from determinantal curves
Groups are fundamental entities in mathematics and in the sciences, which, when viewed as symmetries of objects, can help understand better or tell the objects in question apart. As "most groups are p-groups", we are motivated to understand structure and symmetries of p-groups, even though
From playlist Research Spotlight

Parahoric Torsors and Degeneration of Moduli Spaces by Vikraman Balaji
Program Quantum Fields, Geometry and Representation Theory 2021 (ONLINE) ORGANIZERS: Aswin Balasubramanian (Rutgers University, USA), Indranil Biswas (TIFR, india), Jacques Distler (The University of Texas at Austin, USA), Chris Elliott (University of Massachusetts, USA) and Pranav Pandi
From playlist Quantum Fields, Geometry and Representation Theory 2021 (ONLINE)

Boundaries of quasi-Fuchsian spaces and continuous/discontinuous (Lecture -1) by Ken'ichi Ohshika
Geometry, Groups and Dynamics (GGD) - 2017 DATE: 06 November 2017 to 24 November 2017 VENUE: Ramanujan Lecture Hall, ICTS, Bengaluru The program focuses on geometry, dynamical systems and group actions. Topics are chosen to cover the modern aspects of these areas in which research has b
From playlist Geometry, Groups and Dynamics (GGD) - 2017

What is a Group? | Abstract Algebra
Welcome to group theory! In today's lesson we'll be going over the definition of a group. We'll see the four group axioms in action with some examples, and some non-examples as well which violate the axioms and are thus not groups. In a fundamental way, groups are structures built from s
From playlist Abstract Algebra

Jacob explains the fundamental concepts in group theory of what groups and subgroups are, and highlights a few examples of groups you may already know. Abelian groups are named in honor of Niels Henrik Abel (https://en.wikipedia.org/wiki/Niels_Henrik_Abel), who pioneered the subject of
From playlist Basics: Group Theory
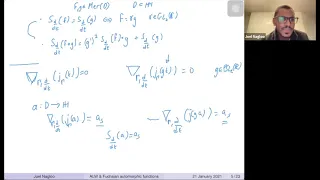
Ax-Lindemann-Weierstrass Theorem (ALW) for Fuchsian automorphic functions - Joel Nagloo
Joint IAS/Princeton University Number Theory Seminar Topic: Ax-Lindemann-Weierstrass Theorem (ALW) for Fuchsian automorphic functions Speaker: Joel Nagloo Affiliation: City University of New York Date: January 21, 2021 For more video please visit http://video.ias.edu
From playlist Mathematics

Representations of Fuchsian groups, parahoric group schemes by Vikraman Balaji
DISCUSSION MEETING : MODULI OF BUNDLES AND RELATED STRUCTURES ORGANIZERS : Rukmini Dey and Pranav Pandit DATE : 10 February 2020 to 14 February 2020 VENUE : Ramanujan Lecture Hall, ICTS, Bangalore Background: At its core, much of mathematics is concerned with the problem of classif
From playlist Moduli Of Bundles And Related Structures 2020

G. McShane - Volumes of hyperbolics manifolds and translation distances
Schlenker and Krasnov have established a remarkable Schlaffli-type formula for the (renormalized) volume of a quasi-Fuchsian manifold. Using this, some classical results in complex analysis and Gromov-Hausdorff convergence for sequences of open 3-manifolds due to Brock-Bromberg one obtain
From playlist Ecole d'été 2016 - Analyse géométrique, géométrie des espaces métriques et topologie

A. Wright - Nearly Fuchsian surface subgroups of finite covolume Kleinian groups
Multicurves have played a fundamental role in the study of mapping class groups of surfaces since the work of Dehn. A beautiful method of describing such systems on the n-punctured disk is given by the Dynnikov coordinate system. In this talk we describe polynomial time algorithms for cal
From playlist Ecole d'été 2018 - Teichmüller dynamics, mapping class groups and applications

Representation theory: Frobenius groups
We recall the definition of a Frobenius group as a transitive permutation group such that any element fixing two points is the identity. Then we prove Frobenius's theorem that the identity together with the elements fixing no points is a normal subgroup. The proof uses induced representati
From playlist Representation theory

Rigidity & flexibility of entropies of boundary maps associated to Fuchsian groups Prof. Katok (PSU)
http://math.columbia.edu/~walterfest/walterfest2020/abstracts/katok.html