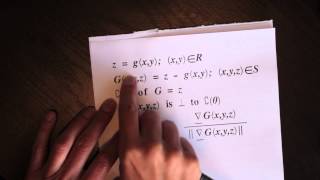Floating point types | Computer arithmetic
Extended precision
Extended precision refers to floating-point number formats that provide greater precision than the basic floating-point formats. Extended precision formats support a basic format by minimizing roundoff and overflow errors in intermediate values of expressions on the base format. In contrast to extended precision, arbitrary-precision arithmetic refers to implementations of much larger numeric types (with a storage count that usually is not a power of two) using special software (or, rarely, hardware). (Wikipedia).