
(IC 5.6) Encoder for arithmetic coding (infinite-precision)
Pseudocode for the arithmetic coding algorithm, assuming addition and multiplication can be done exactly (i.e. with infinite precision). Later we modify this to work with finite precision. A playlist of these videos is available at: http://www.youtube.com/playlist?list=PLE125425EC837
From playlist Information theory and Coding

(IC 5.12) Finite-precision arithmetic coding - Setup
Pre-defining the quantities that will be needed in the finite-precision algorithm. A playlist of these videos is available at: http://www.youtube.com/playlist?list=PLE125425EC837021F
From playlist Information theory and Coding

Eva Darulova : Programming with numerical uncertainties
Abstract : Numerical software, common in scientific computing or embedded systems, inevitably uses an approximation of the real arithmetic in which most algorithms are designed. Finite-precision arithmetic, such as fixed-point or floating-point, is a common and efficient choice, but introd
From playlist Mathematical Aspects of Computer Science

Measurement, approximation and interval arithmetic (I) | Real numbers and limits Math Foundations 81
This video introduces interval arithmetic, first in the context of natural numbers, and then for integers. We start with some remarks from the previous video on the difficulties with irrational numbers, sqrt(2), pi and e. Then we give some general results about order (less than, greater
From playlist Math Foundations
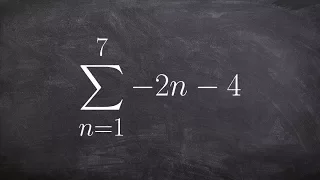
Learn to use summation notation for an arithmetic series to find the sum
👉 Learn how to find the partial sum of an arithmetic series. A series is the sum of the terms of a sequence. An arithmetic series is the sum of the terms of an arithmetic sequence. The formula for the sum of n terms of an arithmetic sequence is given by Sn = n/2 [2a + (n - 1)d], where a is
From playlist Series

Difficulties with real numbers as infinite decimals ( I) | Real numbers + limits Math Foundations 91
There are three quite different approaches to the idea of a real number as an infinite decimal. In this lecture we look carefully at the first and most popular idea: that an infinite decimal can be defined in terms of an infinite sequence of digits appearing to the right of a decimal point
From playlist Math Foundations
(IC 5.11) Finite-precision arithmetic coding - Rescaling
We integrate the rescaling operations into the infinite-precision encoder, as a precursor to the finite-precision encoder. A playlist of these videos is available at: http://www.youtube.com/playlist?list=PLE125425EC837021F
From playlist Information theory and Coding
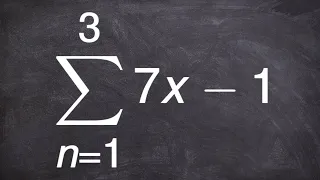
Finding the sum or an arithmetic series using summation notation
👉 Learn how to find the partial sum of an arithmetic series. A series is the sum of the terms of a sequence. An arithmetic series is the sum of the terms of an arithmetic sequence. The formula for the sum of n terms of an arithmetic sequence is given by Sn = n/2 [2a + (n - 1)d], where a is
From playlist Series

Faster Arbitrary Precision Computation of Elementary Functions
For the latest information, please visit: http://www.wolfram.com Speaker: Mark Sofroniou Wolfram developers and colleagues discussed the latest in innovative technologies for cloud computing, interactive deployment, mobile devices, and more.
From playlist Wolfram Technology Conference 2015

Elementary Numerical Analysis by Prof. Rekha P. Kulkarni,Department of Mathematics,IIT Bombay.For more details on NPTEL visit http://nptel.ac.in
From playlist NPTEL: Elementary Numerical Analysis | CosmoLearning Mathematics

Your Daily Equation #22: 8 - 2 ÷ 2 x 3 + 4 = ?
Episode 22 #YourDailyEquation: Simple arithmetic problems go viral with people proposing all sorts of different answers. It speaks to an important concept--the order of various operations matters--but, as Brian Greene discusses, is often taught in a less-than-inspirational way in the class
From playlist Your Daily Equation with Brian Greene
Overview of Numerical Computation
This talk will be an introduction to and summary of many of the numerical computation capabilities built into Mathematica, including arbitrary precision arithmetic, numerical linear algebra, optimization, integration, and differential equations.
From playlist Wolfram Technology Conference 2013

Local-global compatibility in the crystalline case - Ana Caraiani
Joint IAS/Princeton University Number Theory Seminar Topic: Local-global compatibility in the crystalline case Speaker: Ana Caraiani Affiliation: Imperial College Date: April 16, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

A Non-flag Arithmetic Regularity Lemma and Counting Lemma - Daniel Altman
Special Year Informal Seminar Topic: A Non-flag Arithmetic Regularity Lemma and Counting Lemma Speaker: Daniel Altman Affiliation: University of Oxford Date: March 10, 2023 We will discuss a version of the Green--Tao arithmetic regularity lemma and counting lemma which works in the gener
From playlist Mathematics

For the latest information, please visit: http://www.wolfram.com Speaker: Mark Sofroniou Wolfram developers and colleagues discussed the latest in innovative technologies for cloud computing, interactive deployment, mobile devices, and more.
From playlist Wolfram Technology Conference 2016
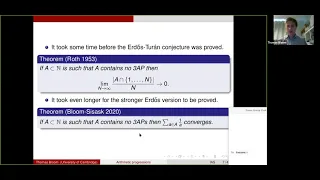
Arithmetic progressions and spectral structure - Thomas Bloom
Computer Science/Discrete Mathematics Seminar II Topic: Arithmetic progressions and spectral structure Speaker: Thomas Bloom Affiliation: University of Cambridge Date: October 13, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

(IC 5.7) Decoder for arithmetic coding (infinite-precision)
Pseudocode for the arithmetic coding algorithm, assuming addition and multiplication can be done exactly (i.e. with infinite precision). Later we modify this to work with finite precision. A playlist of these videos is available at: http://www.youtube.com/playlist?list=PLE125425EC837021F
From playlist Information theory and Coding
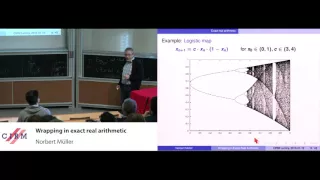
Norbert Müller : Wrapping in exact real arithmetic
Abstract : A serious problem common to all interval algorithms is that they suffer from wrapping effects, i.e. unnecessary growth of approximations during a computation. This is essentially connected to functional dependencies inside vectors of data computed from the same inputs. Reducing
From playlist SPECIAL 7th European congress of Mathematics Berlin 2016.

