
Solving an exponential equation using the one to one property 16^x + 2 = 6
👉 Learn how to solve exponential equations. An exponential equation is an equation in which a variable occurs as an exponent. To solve an exponential equation, we isolate the exponential part of the equation. Then we take the log of both sides. Note that the base of the log should correspo
From playlist Solve Exponential Equations with Logarithms
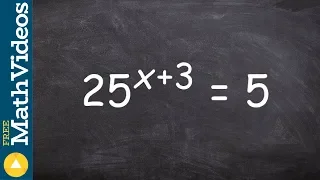
Using one to one property when exponents do not have the same base, 25^(x+3) = 5
👉 Learn how to solve exponential equations. An exponential equation is an equation in which a variable occurs as an exponent. To solve an exponential equation, we isolate the exponential part of the equation. Then we take the log of both sides. Note that the base of the log should correspo
From playlist Solve Exponential Equations without a Calculator

Determine Exponential Function Values and Graph the Function
This video explains how to determine exponential function values. The function values are then used to graph the exponential function. http://mathispower4u.com
From playlist Introduction to Exponential Functions
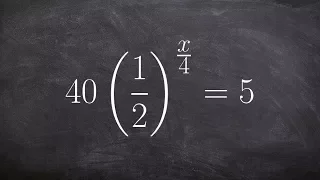
Solving exponential equations using the one to one property
👉 Learn how to solve exponential equations. An exponential equation is an equation in which a variable occurs as an exponent. To solve an exponential equation, we isolate the exponential part of the equation. Then we take the log of both sides. Note that the base of the log should correspo
From playlist Solve Exponential Equations with Logarithms

Solving an exponential equation using the one to one property
👉 Learn how to solve exponential equations. An exponential equation is an equation in which a variable occurs as an exponent. To solve an exponential equation, we isolate the exponential part of the equation. Then we take the log of both sides. Note that the base of the log should correspo
From playlist Solve Exponential Equations with Logarithms

Learn basics for solving an exponential equation by using one to one property
👉 Learn how to solve exponential equations. An exponential equation is an equation in which a variable occurs as an exponent. To solve an exponential equation, we isolate the exponential part of the equation. Then we take the log of both sides. Note that the base of the log should correspo
From playlist Solve Exponential Equations with Logarithms
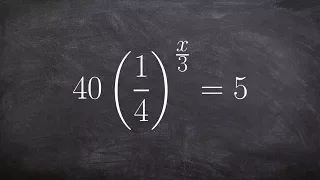
Solve an exponential equation using one to one property and isolating the exponent
👉 Learn how to solve exponential equations. An exponential equation is an equation in which a variable occurs as an exponent. To solve an exponential equation, we isolate the exponential part of the equation. Then we take the log of both sides. Note that the base of the log should correspo
From playlist Solve Exponential Equations with Logarithms
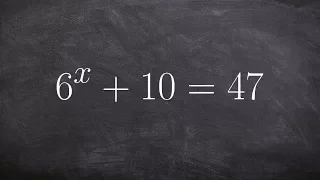
Solving an exponential equation by using change of base for logarithms
👉 Learn how to solve exponential equations. An exponential equation is an equation in which a variable occurs as an exponent. To solve an exponential equation, we isolate the exponential part of the equation. Then we take the log of both sides. Note that the base of the log should correspo
From playlist Solve Exponential Equations with Logarithms
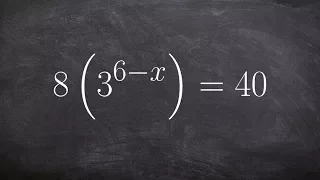
Using inverse properties to solve an exponential equation
👉 Learn how to solve exponential equations. An exponential equation is an equation in which a variable occurs as an exponent. To solve an exponential equation, we isolate the exponential part of the equation. Then we take the log of both sides. Note that the base of the log should correspo
From playlist Solve Exponential Equations with Logarithms

8ECM Invited Lecture: Emmanuel Kowalski
From playlist 8ECM Invited Lectures

Rumours, consensus and epidemics on networks (Lecture 1) by A Ganesh
PROGRAM : ADVANCES IN APPLIED PROBABILITY ORGANIZERS : Vivek Borkar, Sandeep Juneja, Kavita Ramanan, Devavrat Shah and Piyush Srivastava DATE & TIME : 05 August 2019 to 17 August 2019 VENUE : Ramanujan Lecture Hall, ICTS Bangalore Applied probability has seen a revolutionary growth in r
From playlist Advances in Applied Probability 2019
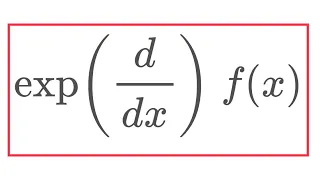
In this video, I define the exponential derivative of a function using power series, and then show something really neat: For “most” functions (those that have a power series expansion), the exponential derivative is just shifting the function by 1! I also derive the product rule for exp
From playlist Calculus

CTNT 2020 - Sieves (by Brandon Alberts) - Lecture 4
The Connecticut Summer School in Number Theory (CTNT) is a summer school in number theory for advanced undergraduate and beginning graduate students, to be followed by a research conference. For more information and resources please visit: https://ctnt-summer.math.uconn.edu/
From playlist CTNT 2020 - Sieves (by Brandon Alberts)

Lecture 20 | The Fourier Transforms and its Applications
Lecture by Professor Brad Osgood for the Electrical Engineering course, The Fourier Transforms and its Applications (EE 261). Professor Osgood continues his lecture on the Discrete Fourier Transform. The Fourier transform is a tool for solving physical problems. In this course the emph
From playlist Lecture Collection | The Fourier Transforms and Its Applications

Neural Networks from Scratch - P.6 Softmax Activation
The what and why of the Softmax Activation function with deep learning. Neural Networks from Scratch book: https://nnfs.io Playlist for this series: https://www.youtube.com/playlist?list=PLQVvvaa0QuDcjD5BAw2DxE6OF2tius3V3 Channel membership: https://www.youtube.com/channel/UCfzlCWGWYyIQ
From playlist Neural Networks from Scratch in Python

Simon Myerson: Repulsion: a how-to guide, Lecture I
Consider the integral zeroes of one or more, not necessarily diagonal, integral polynomials in many variables with the same degree. The basic principles for applying the circle method here were laid out by Birch. One way to improve on his work is repulsion: showing that the exponential sum
From playlist Hausdorff School "The Circle Method"

Lecture 22 | The Fourier Transforms and its Applications
Lecture by Professor Brad Osgood for the Electrical Engineering course, The Fourier Transforms and its Applications (EE 261). Professor Osgood lectures on the basics of the fast Fourier transforms algorithm The Fourier transform is a tool for solving physical problems. In this course
From playlist Lecture Collection | The Fourier Transforms and Its Applications
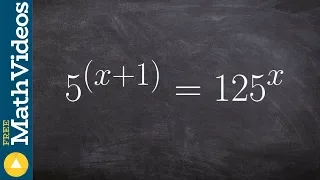
Solving an equation using the one to one property of exponents 5^(x+1) = 125^x
👉 Learn how to solve exponential equations. An exponential equation is an equation in which a variable occurs as an exponent. To solve an exponential equation, we isolate the exponential part of the equation. Then we take the log of both sides. Note that the base of the log should correspo
From playlist Solve Exponential Equations without a Calculator

