
What is a Tensor? Lesson 11: The metric tensor
What is a Tensor 11: The Metric Tensor
From playlist What is a Tensor?

Calculus 3: Tensors (1 of 28) What is a Tensor?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what is a tensor. A tensor is a mathematical representation of a scalar (tensor of rank 0), a vector (tensor of rank 1), a dyad (tensor of rank 2), a triad (tensor or rank 3). Next video in t
From playlist CALCULUS 3 CH 10 TENSORS
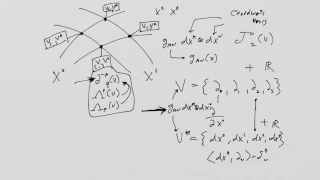
What is a Tensor? Lesson 29: Transformations of tensors and p-forms (part review)
What is a Tensor? Lesson 29: Tensor and N-form Transformations This long lesson begins with a review of tensor product spaces and the relationship between coordinate transformations on spacetime and basis transformations of tensor fields. Then we do a full example to introduce the idea th
From playlist What is a Tensor?
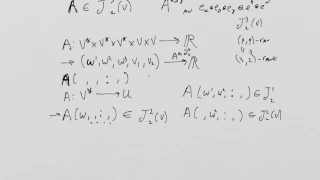
What is a Tensor? Lesson 12 (redux): Contraction and index gymnastics
What is a Tensor? Lesson 12 (redux): Contraction and index gymnastics I have redone the index gymnastics lecture to try and fill in the details regarding contractions. I will keep them both in the playlist for now.
From playlist What is a Tensor?

What is General Relativity? Lesson 68: The Einstein Tensor
What is General Relativity? Lesson 68: The Einstein Tensor The Einstein tensor defined! Using the Ricci tensor and the curvature scalar we can calculate the curvature scalar of a slice of a manifold using the Einstein tensor. Please consider supporting this channel via Patreon: https:/
From playlist What is General Relativity?

Derived structures controlling representations - Carl Wang-Erickson
More videos on http://video.ias.edu
From playlist Mathematics

GPDE Workshop Some Rigidity Results Using Full Non Linear Equations Djadli hi
Zindine Djadli University of France, Grenoble February 26, 2009 For more videos, visit http://video.ias.edu
From playlist Mathematics

What is a Tensor 5: Tensor Products
What is a Tensor 5: Tensor Products Errata: At 22:00 I write down "T_00 e^0 @ e^1" and the correct expression is "T_00 e^0 @ e^0"
From playlist What is a Tensor?

MIT 3.60 | Lec 15b: Symmetry, Structure, Tensor Properties of Materials
Part 2: Space Group Notation and Tensors View the complete course at: http://ocw.mit.edu/3-60F05 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 3.60 Symmetry, Structure & Tensor Properties of Material

Tensile Strength Challenge: Cotton vs. Steel - Christmas Lectures with Charles Stirling
There are situations where cotton is stronger than steel. Watch the full fifth lecture of the series: https://www.rigb.org/christmas-lectures/watch/1992/our-world-through-the-looking-glass/in-the-hands-of-the-giants?utm_source=youtube&utm_medium=social&utm_term=description Charles Stirlin
From playlist Highlights from the Christmas Lectures Archive
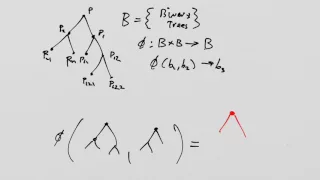
What is a Tensor? Lesson 19: Algebraic Structures I
What is a Tensor? Lesson 19: Algebraic Structures Part One: Groupoids to Fields This is a redo or a recently posted lesson. Same content, a bit cleaner. Algebraic structures are frequently mentioned in the literature of general relativity, so it is good to understand the basic lexicon of
From playlist What is a Tensor?

Branched Holomorphic Cartan Geometries by Sorin Dumitrescu
DISCUSSION MEETING ANALYTIC AND ALGEBRAIC GEOMETRY DATE:19 March 2018 to 24 March 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore. Complex analytic geometry is a very broad area of mathematics straddling differential geometry, algebraic geometry and analysis. Much of the interactions be
From playlist Analytic and Algebraic Geometry-2018
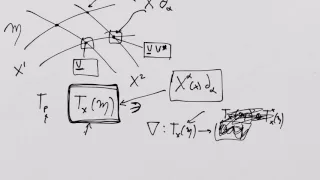
What is a Tensor? Lesson 16: The metric tensor field
What is a Tensor? Lesson 16: The metric tensor field
From playlist What is a Tensor?

Livine Etera : The Geometry of Loop Quantum Gravity
Recording during the thematic meeting : "Geometrical and Topological Structures of Information" the August 31, 2017 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent
From playlist Geometry
Rod Gover - An introduction to conformal geometry and tractor calculus (Part 3)
After recalling some features (and the value of) the invariant « Ricci calculus » of pseudo‐Riemannian geometry, we look at conformal rescaling from an elementary perspective. The idea of conformal covariance is visited and some covariant/invariant equations from physics are recovered in
From playlist Ecole d'été 2014 - Analyse asymptotique en relativité générale

Holomorphic Cartan geometries on simply connected manifolds by Sorin Dumitrescu
Discussion Meeting Complex Algebraic Geometry ORGANIZERS: Indranil Biswas, Mahan Mj and A. J. Parameswaran DATE:01 October 2018 to 06 October 2018 VENUE: Madhava Lecture Hall, ICTS, Bangalore The discussion meeting on Complex Algebraic Geometry will be centered around the "Infosys-ICT
From playlist Complex Algebraic Geometry 2018

A hitchin-kobayashi correspondance for generalized seiberg-witten equations by Varun Thakre
Program : Integrable systems in Mathematics, Condensed Matter and Statistical Physics ORGANIZERS : Alexander Abanov, Rukmini Dey, Fabian Essler, Manas Kulkarni, Joel Moore, Vishal Vasan and Paul Wiegmann DATE & TIME : 16 July 2018 to 10 August 2018 VENUE : Ramanujan L
From playlist Integrable systems in Mathematics, Condensed Matter and Statistical Physics

Cosmological Perturbation Theory / CMB (Lecture 2) by D Pogosyan
Program Cosmology - The Next Decade ORGANIZERS : Rishi Khatri, Subha Majumdar and Aseem Paranjape DATE : 03 January 2019 to 25 January 2019 VENUE : Ramanujan Lecture Hall, ICTS Bangalore The great observational progress in cosmology has revealed some very intriguing puzzles, the most i
From playlist Cosmology - The Next Decade

What Is A Tensor Lesson #1: Elementary vector spaces
We define a vector space and lay the foundation of a solid understanding of tensors.
From playlist What is a Tensor?
