
What is an Injective Function? Definition and Explanation
An explanation to help understand what it means for a function to be injective, also known as one-to-one. The definition of an injection leads us to some important properties of injective functions! Subscribe to see more new math videos! Music: OcularNebula - The Lopez
From playlist Functions

Definition of an Injective Function and Sample Proof
We define what it means for a function to be injective and do a simple proof where we show a specific function is injective. Injective functions are also called one-to-one functions. Useful Math Supplies https://amzn.to/3Y5TGcv My Recording Gear https://amzn.to/3BFvcxp (these are my affil
From playlist Injective, Surjective, and Bijective Functions

Proof of the Convolution Theorem
Proof of the Convolution Theorem, The Laplace Transform of a convolution is the product of the Laplace Transforms, changing order of the double integral, proving the convolution theorem, www.blackpenredpen.com
From playlist Convolution & Laplace Transform (Nagle Sect7.7)

Why Biodiversity Is Good For The Economy
Research suggests that more diverse ecosystems are better for the bottom line. Thanks to the University of Minnesota for sponsoring this video! http://twin-cities.umn.edu/ Credits (and Twitter handles): Script Writer: Peter Reich Script Editor: Kate Yoshida (@KateYoshida) Video Illustr
From playlist Society, Culture & Technology

Desperate Battle: USS Borie vs U-405
By October 1943, the tide in the Battle of the Atlantic had turned, and the allies had shifted from fighting on the defensive to taking the battle to the U-boats themselves. But fishing for U-boats in millions of miles of ocean was a daunting task, and a dangerous one, as the officers and
From playlist Tin Cans: Stories of WWII Destroyers

The idea of ‘atonement’ sounds very old-fashioned and is deeply rooted in religious tradition. To atone means, in essence, to acknowledge one’s capacity for wrongness and one’s readiness for apology and desire for change. It’s a concept that every society needs at its center. For gifts and
From playlist RELATIONSHIPS

Abstract Algebra: The definition of a Ring
Learn the definition of a ring, one of the central objects in abstract algebra. We give several examples to illustrate this concept including matrices and polynomials. Be sure to subscribe so you don't miss new lessons from Socratica: http://bit.ly/1ixuu9W ♦♦♦♦♦♦♦♦♦♦ We recommend th
From playlist Abstract Algebra
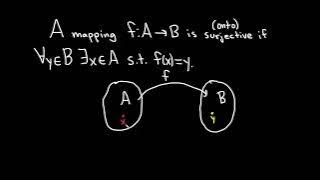
Definition of a Surjective Function and a Function that is NOT Surjective
We define what it means for a function to be surjective and explain the intuition behind the definition. We then do an example where we show a function is not surjective. Surjective functions are also called onto functions. Useful Math Supplies https://amzn.to/3Y5TGcv My Recording Gear ht
From playlist Injective, Surjective, and Bijective Functions

Jason Isbell and the 400 Unit - Middle Of The Morning (Official Lyric Video)
'Weathervanes,' the new album from Jason Isbell and the 400 Unit, will be available everywhere on June 9th, 2023. Pre-order here: https://orcd.co/weathervanes
From playlist 🆕🎧 New Alternative 40 Chart | Updated Weekly

Francesco Ciraulo: Notions of Booleanization in pointfree Topology
The lecture was held within the framework of the Hausdorff Trimester Program: Types, Sets and Constructions. Abstract: Boolean algebras play a key role in the foundations of classical mathematics. And a similar role is played by Heyting algebras for constructive mathematics. But this is
From playlist Workshop: "Constructive Mathematics"

Thanks to 23andMe for sponsoring this video! http://www.23andme.com/minuteearth Snakes occupy a special place in the human brain because they’re so weird. Thanks also to our supporters on https://www.patreon.com/MinuteEarth ___________________________________________ FYI: We try to lea
From playlist Evolution

Differential Equations | Convolution: Definition and Examples
We give a definition as well as a few examples of the convolution of two functions. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Differential Equations

Equivalence Relations Definition and Examples
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Equivalence Relations Definition and Examples. This video starts by defining a relation, reflexive relation, symmetric relation, transitive relation, and then an equivalence relation. Several examples are given.
From playlist Abstract Algebra

Why Are Some Animals Venomous?
Viewers like you help make PBS (Thank you 😃) . Support your local PBS Member Station here: https://to.pbs.org/PBSDSDonate Check out “Venomous” by Christie Wilcox: http://bit.ly/VenomousBook Help us translate this video! http://www.youtube.com/timedtext_video?ref=share&v=Qd92MuVZXik ↓ Mor
From playlist Be Smart - LATEST EPISODES!

Paul André Melliès: Refinement type systems and Martin Lof type theory
Please Note: Due to technical issues the recordings of the blackboard are shown in a slideshow manner. The lecture was held within the framework of the Hausdorff Trimester Program: Types, Sets and Constructions. Abstract: In this talk, I will review my recent work with Noam Zeilberger on
From playlist Workshop: "Types, Homotopy, Type theory, and Verification"

Laura Ciobanu: Formal conjugacy growth and hyperbolicity
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebra

Abstract Algebra | What is a ring?
We give the definition of a ring and present some examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Splitting of Conjugacy Classes in Normal Subgroups
This was recorded as supplemental content for Math 110AH at UCLA in Fall 2020. In this video, we investigate the relationship between conjugacy classes and normal subgroups. 0:00 Setup 3:14 General theory 15:49 Example: A_5
From playlist Group Theory

Is the function continuous or not
👉 Learn how to determine whether a function is continuos or not. A function is said to be continous if two conditions are met. They are: the limit of the function exist and that the value of the function at the point of continuity is defined and is equal to the limit of the function. Other
From playlist Is the Functions Continuous or Not?

The Conjugacy Class Equation Proof
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys The Conjugacy Class Equation Proof
From playlist Abstract Algebra