
Joel David Hamkins : The hierarchy of second-order set theories between GBC and KM and beyond
Abstract: Recent work has clarified how various natural second-order set-theoretic principles, such as those concerned with class forcing or with proper class games, fit into a new robust hierarchy of second-order set theories between Gödel-Bernays GBC set theory and Kelley-Morse KM set th
From playlist Logic and Foundations
A new basis theorem for ∑13 sets
Distinguished Visitor Lecture Series A new basis theorem for ∑13 sets W. Hugh Woodin Harvard University, USA and University of California, Berkeley, USA
From playlist Distinguished Visitors Lecture Series

Distinguished Visitor Lecture Series Finding randomness Theodore A. Slaman University of California, Berkeley, USA
From playlist Distinguished Visitors Lecture Series

Counting Woodin cardinals in HOD
Distinguished Visitor Lecture Series Counting Woodin cardinals in HOD W. Hugh Woodin Harvard University, USA and University of California, Berkeley, USA
From playlist Distinguished Visitors Lecture Series

Here I prove the Heine-Borel Theorem, one of the most fundamental theorems in analysis. It says that in R^n, all boxes must be compact. The proof itself is very neat, and uses a bisection-type argument. Enjoy! Topology Playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmA13vj9xkHG
From playlist Topology

Evaluate the limit with tangent
👉 Learn how to evaluate the limit of a function involving trigonometric expressions. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The limit of a function is usually evaluated by direct
From playlist Evaluate Limits with Trig

Characterization of the determinant
In this video, I show why the determinant is so special in math: Namely, it is the only function which is multilinear, alternating, and has the value 1 at the identity matrix. This is a generalization of a previous matrix puzzle for the 2 x 2 case. 2 x 2 case: https://youtu.be/lIMeIC1ZJO8
From playlist Determinants

Gabriel Goldberg: The Jackson analysis and the strongest hypotheses
HYBRID EVENT Recorded during the meeting "XVI International Luminy Workshop in Set Theory" the September 13, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematician
From playlist Logic and Foundations

L'Hopital's Rule sine x over x
👉 Learn how to evaluate the limit of a function involving trigonometric expressions. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The limit of a function is usually evaluated by direct
From playlist Evaluate Limits with Trig

Find the value the limits with cosine
👉 Learn how to evaluate the limit of a function involving trigonometric expressions. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The limit of a function is usually evaluated by direct
From playlist Evaluate Limits with Trig
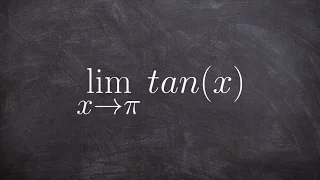
Learn to evaluate the limit of tangent
👉 Learn how to evaluate the limit of a function involving trigonometric expressions. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The limit of a function is usually evaluated by direct
From playlist Evaluate Limits with Trig
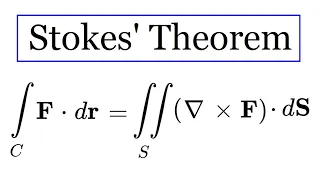
In this video, I present another example of Stokes theorem, this time using it to calculate the line integral of a vector field. It is a very useful theorem that arises a lot in physics, for example in Maxwell's equations. Other Stokes Example: https://youtu.be/-fYbBSiqvUw Yet another Sto
From playlist Vector Calculus

Wojciech Kucharz: Criteria for equivalence between power series and polynomials
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebraic and Complex Geometry

Set Theory - What is Set Theory and what is it for? Oxford Mathematics 3rd Year Student Lecture
This is the first of four lectures from Robin Knight's 3rd Year Set Theory course. Robin writes: "Infinity baffled mathematicians, and everyone else, for thousands of years. But around 1870, Georg Cantor worked out how to study infinity in a way that made sense, and created set theory. Mo
From playlist Oxford Mathematics Student Lectures - Set Theory

(PP 1.8) Measure theory: CDFs and Borel Probability Measures
Correspondence between Borel probability measures on R and CDFs (cumulative distribution functions). A playlist of the Probability Primer series is available here: http://www.youtube.com/view_play_list?p=17567A1A3F5DB5E4 You can skip the measure theory (Section 1) if you're not in
From playlist Probability Theory

Evaluate the limit using special trigonometric limit of cosine
👉 Learn how to evaluate the limit of a function involving trigonometric expressions. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The limit of a function is usually evaluated by direct
From playlist Evaluate Limits with Trig

Use limit laws and special trig limits to evaluate
👉 Learn how to evaluate the limit of a function involving trigonometric expressions. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The limit of a function is usually evaluated by direct
From playlist Evaluate Limits with Trig

Differential Isomorphism and Equivalence of Algebraic Varieties Board at 49:35 Sum_i=1^N 2/(x-phi_i(y,t))^2
From playlist Fall 2017

Natasha Dobrinen: Borel sets of Rado graphs are Ramsey
The Galvin-Prikry theorem states that Borel partitions of the Baire space are Ramsey. Thus, given any Borel subset $\chi$ of the Baire space and an infinite set $N$, there is an infinite subset $M$ of $N$ such that $\left [M \right ]^{\omega }$ is either contained in $\chi$ or disjoint fr
From playlist Combinatorics

How to apply L'Hopital's Rule to evaluate the limit
👉 Learn how to evaluate the limit of a function involving trigonometric expressions. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The limit of a function is usually evaluated by direct
From playlist Evaluate Limits with Trig