
Kevin Hendrey - Obstructions to bounded branch-depth in matroids (CMSA Combinatorics Seminar)
Kevin Hendrey (Institute for Basic Science) presents “Obstructions to bounded branch-depth in matroids”, 24 November 2020 (CMSA Combinatorics Seminar).
From playlist CMSA Combinatorics Seminar

Using a set of points determine if the figure is a parallelogram using the midpoint formula
👉 Learn how to determine the figure given four points. A quadrilateral is a polygon with four sides. Some of the types of quadrilaterals are: parallelogram, square, rectangle, rhombus, kite, trapezoid, etc. Each of the types of quadrilateral has its properties. Given four points that repr
From playlist Quadrilaterals on a Coordinate Plane
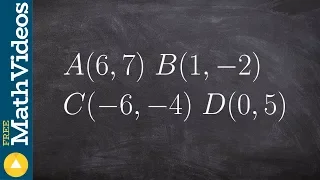
Determining if a set of points makes a parallelogram or not
👉 Learn how to determine the figure given four points. A quadrilateral is a polygon with four sides. Some of the types of quadrilaterals are: parallelogram, square, rectangle, rhombus, kite, trapezoid, etc. Each of the types of quadrilateral has its properties. Given four points that repr
From playlist Quadrilaterals on a Coordinate Plane
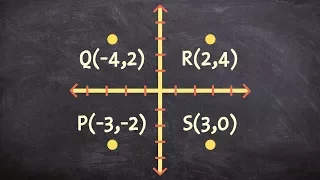
Using the slope formula to determine if points make up a rectangle
👉 Learn how to determine the figure given four points. A quadrilateral is a polygon with four sides. Some of the types of quadrilaterals are: parallelogram, square, rectangle, rhombus, kite, trapezoid, etc. Each of the types of quadrilateral has its properties. Given four points that repr
From playlist Quadrilaterals on a Coordinate Plane

Determine if a set of points is a parallelogram by using the slope formula
👉 Learn how to determine the figure given four points. A quadrilateral is a polygon with four sides. Some of the types of quadrilaterals are: parallelogram, square, rectangle, rhombus, kite, trapezoid, etc. Each of the types of quadrilateral has its properties. Given four points that repr
From playlist Quadrilaterals on a Coordinate Plane

How to determine the perimeter of a quadrilateral using distance formula of four points
👉 Learn how to determine the figure given four points. A quadrilateral is a polygon with four sides. Some of the types of quadrilaterals are: parallelogram, square, rectangle, rhombus, kite, trapezoid, etc. Each of the types of quadrilateral has its properties. Given four points that repr
From playlist Quadrilaterals on a Coordinate Plane

Determine if a set of points is a parallelogram using the distance formula
👉 Learn how to determine the figure given four points. A quadrilateral is a polygon with four sides. Some of the types of quadrilaterals are: parallelogram, square, rectangle, rhombus, kite, trapezoid, etc. Each of the types of quadrilateral has its properties. Given four points that repr
From playlist Quadrilaterals on a Coordinate Plane
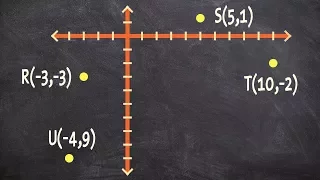
Determine if a set of points is a trapezoid or not
👉 Learn how to determine the figure given four points. A quadrilateral is a polygon with four sides. Some of the types of quadrilaterals are: parallelogram, square, rectangle, rhombus, kite, trapezoid, etc. Each of the types of quadrilateral has its properties. Given four points that repr
From playlist Quadrilaterals on a Coordinate Plane

Determine if a set of points makes up a rectangle using the distance formula
👉 Learn how to determine the figure given four points. A quadrilateral is a polygon with four sides. Some of the types of quadrilaterals are: parallelogram, square, rectangle, rhombus, kite, trapezoid, etc. Each of the types of quadrilateral has its properties. Given four points that repr
From playlist Quadrilaterals on a Coordinate Plane

Joseph Bonin: Delta-matroids as subsystems of sequences of Higgs lifts
Abstract: Delta-matroids generalize matroids. In a delta-matroid, the counterparts of bases, which are called feasible sets, can have different sizes, but they satisfy a similar exchange property in which symmetric differences replace set differences. One way to get a delta-matroid is to t
From playlist Combinatorics

Nonlinear algebra, Lecture 13: "Polytopes and Matroids ", by Mateusz Michalek
This is the thirteenth lecture in the IMPRS Ringvorlesung, the advanced graduate course at the Max Planck Institute for Mathematics in the Sciences.
From playlist IMPRS Ringvorlesung - Introduction to Nonlinear Algebra

Yusuke Kobayashi: A weighted linear matroid parity algorithm
The lecture was held within the framework of the follow-up workshop to the Hausdorff Trimester Program: Combinatorial Optimization. Abstract: The matroid parity (or matroid matching) problem, introduced as a common generalization of matching and matroid intersection problems, is so gener
From playlist Follow-Up-Workshop "Combinatorial Optimization"

Victor Chepoi: Simple connectivity, local to global, and matroids
Victor Chepoi: Simple connectivity, local-to-global, and matroids A basis graph of a matroid M is the graph G(M) having the bases of M as the vertex-set and the pairs of bases differing by an elementary exchange as edges. Basis graphs of matroids have been characterized by S.B. Maurer, J.
From playlist HIM Lectures 2015

Anna De Mier: Approximating clutters with matroids
Abstract: There are several clutters (antichains of sets) that can be associated with a matroid, as the clutter of circuits, the clutter of bases or the clutter of hyperplanes. We study the following question: given an arbitrary clutter Λ, which are the matroidal clutters that are closest
From playlist Combinatorics

Gyula Pap: Linear matroid matching in the oracle model
Gyula Pap: Linear matroid matching in the oracle model Linear matroid matching is understood as a special case of matroid matching when the matroid is given with a matrix representation. However, for certain examples of linear matroids, the matrix representation is not given, and actuall
From playlist HIM Lectures 2015

Zoltán Szigeti: Packing of arborescences with matroid constraints via matroid intersection
The lecture was held within the framework of the follow-up workshop to the Hausdorff Trimester Program: Combinatorial Optimization. Abstract: Edmonds characterized digraphs having a packing of k spanning arborescences in terms of connectivity and later in terms of matroid intersection. D
From playlist Follow-Up-Workshop "Combinatorial Optimization"
Sahil Singla: Online Matroid Intersection Beating Half for Random Arrival
We study a variant of the online bipartite matching problem that we call the online matroid intersection problem. For two matroids M1 and M2 defined on the same ground set E, the problem is to design an algorithm that constructs the largest common independent set in an online fashion. At e
From playlist HIM Lectures 2015

Determining if a set of points is a rhombus, square or rectangle
👉 Learn how to determine the figure given four points. A quadrilateral is a polygon with four sides. Some of the types of quadrilaterals are: parallelogram, square, rectangle, rhombus, kite, trapezoid, etc. Each of the types of quadrilateral has its properties. Given four points that repr
From playlist Quadrilaterals on a Coordinate Plane
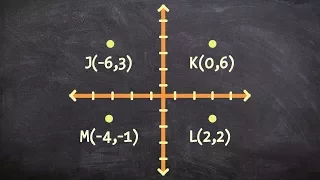
How to determine if a set of points makes up a rectangle using the distance formula
👉 Learn how to determine the figure given four points. A quadrilateral is a polygon with four sides. Some of the types of quadrilaterals are: parallelogram, square, rectangle, rhombus, kite, trapezoid, etc. Each of the types of quadrilateral has its properties. Given four points that repr
From playlist Quadrilaterals on a Coordinate Plane

The log-concavity conjecture and the tropical Laplacian - June Huh
June Huh Princeton University; Veblen Fellow, School of Mathematics February 17, 2015 The log-concavity conjecture predicts that the coefficients of the chromatic (characteristic) polynomial of a matroid form a log-concave sequence. The known proof for realizable matroids uses algebraic g
From playlist Mathematics