
What is the definition of a geometric sequence
👉 Learn about sequences. A sequence is a list of numbers/values exhibiting a defined pattern. A number/value in a sequence is called a term of the sequence. There are many types of sequence, among which are: arithmetic and geometric sequence. An arithmetic sequence is a sequence in which
From playlist Sequences

How to determine the rule for a geometric sequence given two values
👉 Learn how to write the explicit formula for a geometric sequence. A sequence is a list of numbers/values exhibiting a defined pattern. A number/value in a sequence is called a term of the sequence. A geometric sequence is a sequence in which each term of the sequence is obtained by multi
From playlist Sequences

Learn how to determine the sum of a geometric finite series
👉 Learn how to find the geometric sum of a series. A series is the sum of the terms of a sequence. A geometric series is the sum of the terms of a geometric sequence. The formula for the sum of n terms of a geometric sequence is given by Sn = a[(r^n - 1)/(r - 1)], where a is the first term
From playlist Series

Evaluating the partial sum of a geometric series
👉 Learn how to find the geometric sum of a series. A series is the sum of the terms of a sequence. A geometric series is the sum of the terms of a geometric sequence. The formula for the sum of n terms of a geometric sequence is given by Sn = a[(r^n - 1)/(r - 1)], where a is the first term
From playlist Series

Learn about the geometric mean of numbers. The geometric mean of n numbers is the nth root of the product of the numbers. To find the geometric mean of n numbers, we first multiply the numbers and then take the nth root of the product.
From playlist Geometry - GEOMETRIC MEAN
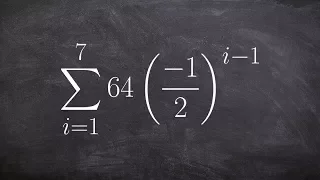
Learning to find the partial sum of a geometric series
👉 Learn how to find the geometric sum of a series. A series is the sum of the terms of a sequence. A geometric series is the sum of the terms of a geometric sequence. The formula for the sum of n terms of a geometric sequence is given by Sn = a[(r^n - 1)/(r - 1)], where a is the first term
From playlist Series
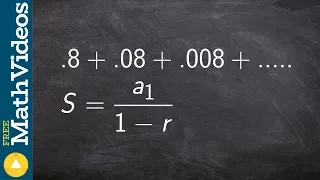
How to determine the infinite sum of a geometric series
👉 Learn how to find the geometric sum of a series. A series is the sum of the terms of a sequence. A geometric series is the sum of the terms of a geometric sequence. The formula for the sum of n terms of a geometric sequence is given by Sn = a[(r^n - 1)/(r - 1)], where a is the first term
From playlist Series
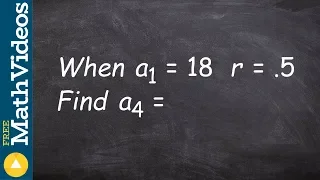
Learn to write the explicit formula for the geometric sequence
👉 Learn how to write the explicit formula for a geometric sequence. A sequence is a list of numbers/values exhibiting a defined pattern. A number/value in a sequence is called a term of the sequence. A geometric sequence is a sequence in which each term of the sequence is obtained by multi
From playlist Sequences
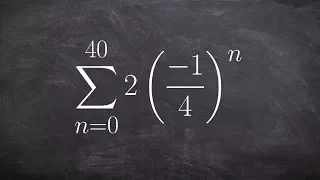
Learn to find the partial sum of a geometric sequence
👉 Learn how to find the geometric sum of a series. A series is the sum of the terms of a sequence. A geometric series is the sum of the terms of a geometric sequence. The formula for the sum of n terms of a geometric sequence is given by Sn = a[(r^n - 1)/(r - 1)], where a is the first term
From playlist Series

Electronic transport properties of the α − T3 lattice by T K Ghosh
DISCUSSION MEETING GEOMETRIC PHASES IN OPTICS AND TOPOLOGICAL MATTER ORGANIZERS: Subhro Bhattacharjee, Joseph Samuel and Supurna Sinha DATE: 21 January 2020 to 24 January 2020 VENUE: Madhava Lecture Hall, ICTS, Bangalore This is a joint ICTS-RRI Discussion Meeting on the geometric pha
From playlist Geometric Phases in Optics and Topological Matter 2020
Boris Apanasov: Non-rigidity for Hyperbolic Lattices and Geometric Analysis
Boris Apanasov, University of Oklahoma Title: Non-rigidity for Hyperbolic Lattices and Geometric Analysis We create a conformal analogue of the M. Gromov-I. Piatetski-Shapiro interbreeding construction to obtain non-faithful representations of uniform hyperbolic 3-lattices with arbitrarily
From playlist 39th Annual Geometric Topology Workshop (Online), June 6-8, 2022

3d N = 4 Super-Yang-Mills on a Lattice by Arthur Lipstein
Nonperturbative and Numerical Approaches to Quantum Gravity, String Theory and Holography DATE:27 January 2018 to 03 February 2018 VENUE:Ramanujan Lecture Hall, ICTS Bangalore The program "Nonperturbative and Numerical Approaches to Quantum Gravity, String Theory and Holography" aims to
From playlist Nonperturbative and Numerical Approaches to Quantum Gravity, String Theory and Holography

Frank Gounelas : Rational curves on K3 surfaces
Bogomolov and Mumford proved that every complex projective K3 surface contains a rational curve. Since then, a lot of progress has been made by Bogomolov, Chen, Hassett, Li, Liedtke, Tschinkel and others, towards the stronger statement that any such surface in fact contains infinitely many
From playlist Algebraic and Complex Geometry

Weakly Modular Functions | The Geometry of SL2,Z, Section 1.4
We provide an alternative motivation for the definition of weakly modular functions. My Twitter: https://twitter.com/KristapsBalodi3 Weakly Modular Functions (0:00) Boring Functions on Compact Riemann Surfaces (2:06) Transforming the Transformation Property (9:15)
From playlist The Geometry of SL(2,Z)

Integral structures on de Rham cohomology
B. Bhatt (IAS) Integral structures on de Rham cohomology Conférence de mi-parcours du programme ANR Théorie de Hodge p-adique et Développements (ThéHopaD) 25-27 septembre 2013 Centre de conférences Marilyn et James Simons IHÉS Bures / Yvette France
From playlist Conférence de mi-parcours du programme ANRThéorie de Hodge p-adique et Développements (ThéHopaD)25-27 septembre 2013

Lec 24 | MIT 6.451 Principles of Digital Communication II
Linear Gaussian Channels View the complete course: http://ocw.mit.edu/6-451S05 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 6.451 Principles of Digital Communication II

Pancharatnam-Zak phase by Vivek Vyas
DISCUSSION MEETING : GEOMETRIC PHASES IN OPTICS AND TOPOLOGICAL MATTER ORGANIZERS : Subhro Bhattacharjee, Joseph Samuel and Supurna Sinha DATE : 21 January 2020 to 24 January 2020 VENUE : Madhava Lecture Hall, ICTS, Bangalore This is a joint ICTS-RRI Discussion Meeting on the geometric
From playlist Geometric Phases in Optics and Topological Matter 2020

Geometric structures and thin groups I - Alan Reid
Speaker: Alan Reid (UT Austin/IAS) Title: Geometric structures and thin groups I Abstract: In these two talks we will discuss situations in which geometric input can be used as a method to certify that a group is thin. This involves a mix of theory and computation. More videos on http://v
From playlist Mathematics

Will Sawin, The freeness alternative to thin sets in Manin's conjecture
VaNTAGe seminar, May 4, 2021 License: CC-BY-NC-SA
From playlist Manin conjectures and rational points
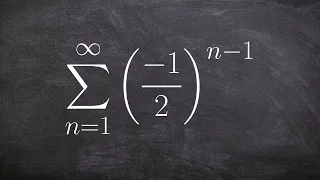
How to determine the sum of a infinite geometric series
👉 Learn how to find the geometric sum of a series. A series is the sum of the terms of a sequence. A geometric series is the sum of the terms of a geometric sequence. The formula for the sum of n terms of a geometric sequence is given by Sn = a[(r^n - 1)/(r - 1)], where a is the first term
From playlist Series