
Vector Auto Regression : Time Series Talk
Let's take a look at the basics of the vector auto regression model in time series analysis! --- Like, Subscribe, and Hit that Bell to get all the latest videos from ritvikmath ~ --- Check out my Medium: https://medium.com/@ritvikmathematics
From playlist Time Series Analysis

11d Machine Learning: Bayesian Linear Regression
Lecture on Bayesian linear regression. By adopting the Bayesian approach (instead of the frequentist approach of ordinary least squares linear regression) we can account for prior information and directly model the distributions of the model parameters by updating with training data. Foll
From playlist Machine Learning

Marcelo Pereyra: Bayesian inference and mathematical imaging - Lecture 4: mixture...
Bayesian inference and mathematical imaging - Part 4: mixture, random fields and hierarchical models Abstract: This course presents an overview of modern Bayesian strategies for solving imaging inverse problems. We will start by introducing the Bayesian statistical decision theory framewo
From playlist Probability and Statistics

(ML 7.1) Bayesian inference - A simple example
Illustration of the main idea of Bayesian inference, in the simple case of a univariate Gaussian with a Gaussian prior on the mean (and known variances).
From playlist Machine Learning

Marcelo Pereyra: Bayesian inference and mathematical imaging - Lecture 1: Bayesian analysis...
Bayesian inference and mathematical imaging - Part 1: Bayesian analysis and decision theory Abstract: This course presents an overview of modern Bayesian strategies for solving imaging inverse problems. We will start by introducing the Bayesian statistical decision theory framework underp
From playlist Probability and Statistics

Autoregressive Models: The Yule-Walker Equations
http://AllSignalProcessing.com for more great signal processing content, including concept/screenshot files, quizzes, MATLAB and data files. The Yule-Walker equations relate the auto covariance of a random signal to the autoregressive (AR) model parameters. They can be used to estimate A
From playlist Random Signal Characterization
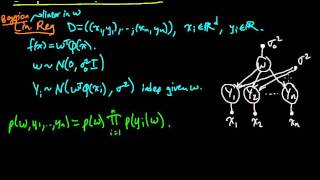
(ML 13.6) Graphical model for Bayesian linear regression
As an example, we write down the graphical model for Bayesian linear regression. We introduce the "plate notation", and the convention of shading random variables which are being conditioned on.
From playlist Machine Learning

The vector cross-product is another form of vector multiplication and results in another vector. In this tutorial I show you a simple way of calculating the cross product of two vectors.
From playlist Introducing linear algebra

NVAE: A Deep Hierarchical Variational Autoencoder (Paper Explained)
VAEs have been traditionally hard to train at high resolutions and unstable when going deep with many layers. In addition, VAE samples are often more blurry and less crisp than those from GANs. This paper details all the engineering choices necessary to successfully train a deep hierarchic
From playlist Papers Explained

Bayesian Time Series : Time Series Talk
Bayesian Stats + Time Series = A World of Fun PyMC3 Intro Video : https://www.youtube.com/watch?v=SP-sAAYvGT8 Link to Code : https://github.com/ritvikmath/YouTubeVideoCode/blob/main/Bayesian%20Time%20Series.ipynb My Patreon : https://www.patreon.com/user?u=49277905
From playlist Time Series Analysis

This shows an interactive illustration that shows vector subtraction. The clip is from the book "Immersive Linear Algebra" at http://www.immersivemath.com.
From playlist Chapter 2 - Vectors

Time Series Forecasting 8 : Vector Autoregression
In this video I cover Vector Autoregressions. Vector autoregressive models are used when you want to predict multiple time series using one model. With them we have to check for stationarity. Convert the data to a stationary form. Then I'll show you how to invert stationarity back to the o
From playlist Time Series Analysis

Noel Cressie: Inference for spatio-temporal changes of arctic sea ice
Abstract: Arctic sea-ice extent has been of considerable interest to scientists in recent years, mainly due to its decreasing trend over the past 20 years. In this talk, I propose a hierarchical spatio-temporal generalized linear model (GLM) for binary Arctic-sea-ice data, where data depen
From playlist Probability and Statistics

Laurent Dinh: "A primer on normalizing flows"
Machine Learning for Physics and the Physics of Learning 2019 Workshop I: From Passive to Active: Generative and Reinforcement Learning with Physics "A primer on normalizing flows" Laurent Dinh, Google Abstract: Normalizing flows are a flexible family of probability distributions that ca
From playlist Machine Learning for Physics and the Physics of Learning 2019

Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention (Paper Explained)
#ai #attention #transformer #deeplearning Transformers are famous for two things: Their superior performance and their insane requirements of compute and memory. This paper reformulates the attention mechanism in terms of kernel functions and obtains a linear formulation, which reduces th
From playlist Papers Explained

Stanford CS330: Multi-Task and Meta-Learning, 2019 | Lecture 5 - Bayesian Meta-Learning
For more information about Stanford’s Artificial Intelligence professional and graduate programs, visit: https://stanford.io/ai Assistant Professor Chelsea Finn, Stanford University http://cs330.stanford.edu/
From playlist Stanford CS330: Deep Multi-Task and Meta Learning

Håvard Rue: Bayesian computation with INLA
Abstract: This talk focuses on the estimation of the distribution of unobserved nodes in large random graphs from the observation of very few edges. These graphs naturally model tournaments involving a large number of players (the nodes) where the ability to win of each player is unknown.
From playlist Probability and Statistics

QRM 7-3: TS for RM 2 (R studio)
Welcome to Quantitative Risk Management (QRM). In the last part of Lesson 7 we play with R studio, to better understand some of the topics we have discussed in the previous videos. We will deal with seasonality, we will simulate and estimate an ARIMA model, and we will perform model selec
From playlist Quantitative Risk Management

This shows an small game that illustrates the concept of a vector. The clip is from the book "Immersive Linear Algebra" at http://www.immersivemath.com
From playlist Chapter 2 - Vectors