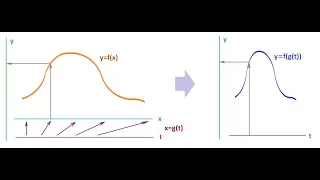
Change of variables and the derivative -- Calculus I
This lecture is on Calculus I. It follows Part I of the book Calculus Illustrated by Peter Saveliev. The text of the book can be found at http://calculus123.com.
From playlist Calculus I

Calculus - The Fundamental Theorem, Part 5
The Fundamental Theorem of Calculus. How an understanding of an incremental change in area helps lead to the fundamental theorem
From playlist Calculus - The Fundamental Theorem of Calculus

What is the Fundamental theorem of Algebra, really? | Abstract Algebra Math Foundations 217
Here we give restatements of the Fundamental theorems of Algebra (I) and (II) that we critiqued in our last video, so that they are now at least meaningful and correct statements, at least to the best of our knowledge. The key is to abstain from any prior assumptions about our understandin
From playlist Math Foundations

Calculus - The Fundamental Theorem, Part 1
The Fundamental Theorem of Calculus. First video in a short series on the topic. The theorem is stated and two simple examples are worked.
From playlist Calculus - The Fundamental Theorem of Calculus

Extended Fundamental Theorem of Calculus
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Extended Fundamental Theorem of Calculus. You can use this instead of the First Fundamental Theorem of Calculus and the Second Fundamental Theorem of Calculus. - Formula - Proof sketch of the formula - Six Examples
From playlist Calculus

Calculus: The Fundamental Theorem of Calculus
This is the second of two videos discussing Section 5.3 from Briggs/Cochran Calculus. In this section, I discuss both parts of the Fundamental Theorem of Calculus. I briefly discuss why the theorem is true, and work through several examples applying the theorem.
From playlist Calculus
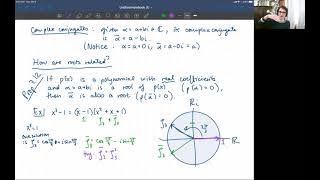
Fundamental Theorem of Algebra
The Fundamental Theorem of Algebra and some additional notes about how roots of polynomials and complex numbers are related to each other.
From playlist Modern Algebra

The Fundamental Theorem of Calculus | Algebraic Calculus One | Wild Egg
In this video we lay out the Fundamental Theorem of Calculus --from the point of view of the Algebraic Calculus. This key result, presented here for the very first time (!), shows how to generalize the Fundamental Formula of the Calculus which we presented a few videos ago, incorporating t
From playlist Algebraic Calculus One

Definitions, specification and interpretation | Arithmetic and Geometry Math Foundations 44
We discuss important meta-issues regarding definitions and specification in mathematics. We also introduce the idea that mathematical definitions, expressions, formulas or theorems may support a variety of possible interpretations. Examples use our previous definitions from elementary ge
From playlist Math Foundations

Smooth base change, smooth and proper base change, lifting varieties, Kunneth
From playlist Étale cohomology and the Weil conjectures

Automorphy Theorems II - David Geraghty
David Geraghty Princeton University; Member, School of Mathematics March 17, 2011 For more videos, visit http://video.ias.edu
From playlist Mathematics

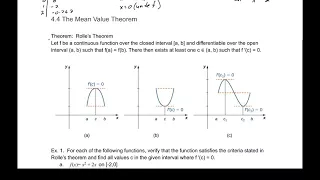
MVT AVT Trapezoidal Sum Related Rates Calculus FRQ
Part A) Estimating Slope of Tangent Line 1:25 Part B) Mean Value Theorem 5:23 Part C) Average Value Theorem and Trapezoidal Sum 11:36 Part D) Related Rates 18:58 PDF's of problems, solutions, and grading commentary at: https://apcentral.collegeboard.org/courses/ap-calculus-ab/exam/past-ex
From playlist AP Calculus AB & BC Style Questions

The special Values of Rankin-Selberg L-functions over a totally Imaginary field by A Raghuram
PROGRAM ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (HYBRID) ORGANIZERS: Ashay Burungale (CalTech/UT Austin, USA), Haruzo Hida (UCLA), Somnath Jha (IIT Kanpur) and Ye Tian (MCM, CAS) DATE: 08 August 2022 to 19 August 2022 VENUE: Ramanujan Lecture Hall and online The program pla
From playlist ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (2022)

On Voevodsky's univalence principle - André Joyal
Vladimir Voevodsky Memorial Conference Topic: On Voevodsky's univalence principle Speaker: André Joyal Affiliation: Université du Québec á Montréal Date: September 11, 2018 For more video please visit http://video.ias.edu
From playlist Mathematics

Automorphy: Potential Automorphy Theorems I
Richard Taylor Harvard University; Distinguished Visiting Professor, School of Mathematics March 10, 2011 For more videos, visit http://video.ias.edu
From playlist Mathematics

On a universal Torelli theorem for elliptic surfaces by CS Rajan
12 December 2016 to 22 December 2016 VENUE : Madhava Lecture Hall, ICTS Bangalore The Birch and Swinnerton-Dyer conjecture is a striking example of conjectures in number theory, specifically in arithmetic geometry, that has abundant numerical evidence but not a complete general solution.
From playlist Theoretical and Computational Aspects of the Birch and Swinnerton-Dyer Conjecture

Distinguished Visitor Lecture Series Finding better randomness Theodore A. Slaman University of California, Berkeley, USA
From playlist Distinguished Visitors Lecture Series

Multisets and a new framework for arithmetic | Data Structures Math Foundations 187
Here we go back to the first videos in this series and recast that discussion in a more solid direction by utilizing our understanding of multisets. The crucial point is to define what a natural number is in a clear way. This issue is far more subtle than is generally acknowledged. For u
From playlist Math Foundations

Proper base change continued, compactly supported cohomology, cohomology with supports, Gysin sequences and purity
From playlist Étale cohomology and the Weil conjectures