
Calculus: Absolute Maximum and Minimum Values
In this video, we discuss how to find the absolute maximum and minimum values of a function on a closed interval.
From playlist Calculus

http://mathispower4u.wordpress.com/
From playlist Solving Absolute Value Equations

Maximum and Minimum Values (Closed interval method)
A review of techniques for finding local and absolute extremes, including an application of the closed interval method
From playlist 241Fall13Ex3

Additive Energy and Vosper's Theorem by David Grynkiewicz
Program Workshop on Additive Combinatorics ORGANIZERS: S. D. Adhikari and D. S. Ramana DATE: 24 February 2020 to 06 March 2020 VENUE: Madhava Lecture Hall, ICTS Bangalore Additive combinatorics is an active branch of mathematics that interfaces with combinatorics, number theory, ergod
From playlist Workshop on Additive Combinatorics 2020
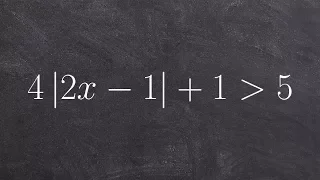
Summary for solving an absolute value inequality
👉 Learn how to solve multi-step absolute value inequalities. The absolute value of a number is the positive value of the number. For instance, the absolute value of 2 is 2 and the absolute value of -2 is also 2. To solve an absolute value inequality where there are more terms apart from th
From playlist Solve Absolute Value Inequalities | Hard
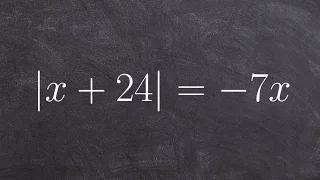
How To Solve an Absolute Value Equation when There is Only One Solution
Learn how to solve absolute value equations with extraneous solutions. Absolute value of a number is the positive value of the number. For instance, the absolute value of 2 is 2 and the absolute value of -2 is also 2. To solve an absolute value problem, we first isolate the absolute value
From playlist Solve Absolute Value Equations

How To Solve an Absolute Value Equation and Test Our Solutions when They Do Not Work
Learn how to solve absolute value equations with extraneous solutions. Absolute value of a number is the positive value of the number. For instance, the absolute value of 2 is 2 and the absolute value of -2 is also 2. To solve an absolute value problem, we first isolate the absolute value
From playlist Solve Absolute Value Equations

Eigenfunction concentration via geodesic beams - Yaiza Canzani
Analysis Seminar Topic: Eigenfunction concentration via geodesic beams Speaker: Yaiza Canzani Affiliation: University of North Carolina Date: May 17, 2021 For more video please visit https://www.ias.edu/video
From playlist Mathematics

Peter SARNAK - Prescribing the spectra of locally uniform geometries
https://ams-ems-smf2022.inviteo.fr/
From playlist International Meeting 2022 AMS-EMS-SMF

On PC-exact saturation - I. Kaplan - Workshop 3 - CEB T1 2018
Itay Kaplan (Hebrew University, Jerusalem) / 30.03.2018 On PC-exact saturation (joint work with Nick Ramsey and Saharon Shelah) A theory T is said to have exact saturation at a (usually singular) cardinal κ if there is a model which is κ- saturated but not κ +- saturated. T has PC-exact
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields

Bounds on Maass spectra from holomorphic forms - Dalimil Mazac
Mathematical Physics Seminar Topic: Bounds on Maass spectra from holomorphic forms Speaker: Dalimil Mazac Affiliation: Member, School of Natural Sciences Date: March 02, 2022 I will discuss new constraints on the spectra of Maass forms on compact hyperbolic 2-orbifolds. The constraints a
From playlist Mathematics

Solving an Absolute Value Equation and Checking for Extraneous Solutions
Learn how to solve absolute value equations with extraneous solutions. Absolute value of a number is the positive value of the number. For instance, the absolute value of 2 is 2 and the absolute value of -2 is also 2. To solve an absolute value problem, we first isolate the absolute value
From playlist Solve Absolute Value Equations
Lucia Mocz: A new Northcott property for Faltings height
Abstract: The Faltings height is a useful invariant for addressing questions in arithmetic geometry. In his celebrated proof of the Mordell and Shafarevich conjectures, Faltings shows the Faltings height satisfies a certain Northcott property, which allows him to deduce his finiteness stat
From playlist Algebraic and Complex Geometry

Learning to solve and graph an absolute value inequality with a rational quantity
👉 Learn how to solve multi-step absolute value inequalities. The absolute value of a number is the positive value of the number. For instance, the absolute value of 2 is 2 and the absolute value of -2 is also 2. To solve an absolute value inequality where there are more terms apart from th
From playlist Solve Absolute Value Inequalities | Hard

Absolute notions in model theory - M. Dzamonja - Workshop 1 - CEB T1 2018
Mirna Dzamonja (East Anglia) / 30.01.2018 The wonderful theory of stability and ranks developed for many notions in first order model theory implies that many model theoretic constructions are absolute, since they can be expressed in terms of internal properties measurable by the existenc
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields

04b Data Analytics Reboot: Statistical Expectation
Lecture on statistical expectation, description, properties and examples. Data Analytics and Geostatistics is an undergraduate course that I teach fall and spring semesters at The University of Texas at Austin. We build up fundamental spatial, subsurface, geoscience and engineering modeli
From playlist Data Analytics and Geostatistics

Arithmetic and Dynamics on Varieties of Markoff Type -Alexander Gamburd
Arithmetic Groups Topic: Arithmetic and Dynamics on Varieties of Markoff Type Speaker: Alexander Gamburd Affiliation: The City University of New York Date: April 13, 2022 The Markoff equation x2+y2+z2=3xyz, which arose in his spectacular thesis (1879), is ubiquitous in a tremendous varie
From playlist Mathematics
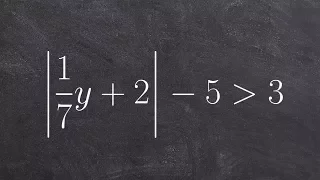
Solving an absolute value inequality by rewriting as a compound inequality
👉 Learn how to solve multi-step absolute value inequalities. The absolute value of a number is the positive value of the number. For instance, the absolute value of 2 is 2 and the absolute value of -2 is also 2. To solve an absolute value inequality where there are more terms apart from th
From playlist Solve Absolute Value Inequalities | Hard

Yuri Manin - Numbers as functions
Numbers as functions
From playlist 28ème Journées Arithmétiques 2013
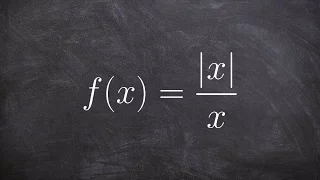
Learn how to evaluate left and right hand limits of a function
👉 Learn how to evaluate the limit of an absolute value function. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The absolute value function is a function which only takes the positive val
From playlist Evaluate Limits of Absolute Value