
What exactly is space? Brian Greene explains what the "stuff" around us is. Subscribe to our YouTube Channel for all the latest from World Science U. Visit our Website: http://www.worldscienceu.com/ Like us on Facebook: https://www.facebook.com/worldscienceu Follow us on Twitter: https:
From playlist Science Unplugged: Physics

"Subscribe to our YouTube Channel for all the latest from World Science U. Visit our Website: http://www.worldscienceu.com/ Like us on Facebook: https://www.facebook.com/worldscienceu Follow us on Twitter: https://twitter.com/worldscienceu"
From playlist Science Unplugged: Special Relativity

B03 Fluid shifts here on earth
The difference between the erect and supine positions here on earth.
From playlist Space Medicine
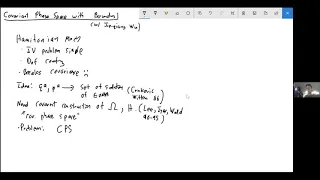
Covariant Phase Space with Boundaries - Daniel Harlow
More videos on http://video.ias.edu
From playlist Natural Sciences

Dimensions (1 of 3: The Traditional Definition - Directions)
More resources available at www.misterwootube.com
From playlist Exploring Mathematics: Fractals

Weird notions of "distance" || Intro to Metric Spaces
Visit https://brilliant.org/TreforBazett/ to get started learning STEM for free, and the first 200 people will get 20% off their annual premium subscription. Check out my MATH MERCH line in collaboration with Beautiful Equations ►https://www.beautifulequation.com/pages/trefor Weird, fun
From playlist Cool Math Series

Ask the Space Lab Expert: What is Space?
Have you ever wanted to go to Space? In this first episode of Space Lab, Brad and Liam from "World of the Orange" take you on an adventure to discover exactly what is Space. You'll find out about the solar system, the big bang, Sci-Fi movies that are becoming reality, and more!
From playlist What is Space? YouTube Space Lab with Liam and Brad

The Human Body in Space - What happens to your body in space? Start learning with Brilliant today for FREE: http://brilliant.org/aperture Follow me on Instagram: https://www.instagram.com/mcewen/ Space is the final frontier. But you know, it’s not like space has a lot going on. There is q
From playlist Science & Technology 🚀

Stable Homotopy Seminar, 8: The Stable Model Category of Spectra
We discuss the enrichment of spectra over spaces, and the compatibility of this enrichment with the model structure. Then we define the stable model structure by adding extra cofibrations to the levelwise model category of spectra, and restricting the weak equivalences to those maps which
From playlist Stable Homotopy Seminar

Stable Homotopy Seminar, 4: Model categories (Ivo Vekemans)
This talk by Ivo Vekemans is a thorough introduction to model categories, presenting: weak factorization systems; the definition of model category and major examples (simplicial sets, topological spaces, and chain complexes); notions of homotopy in a model category, and the homotopy catego
From playlist Stable Homotopy Seminar

Bradley Nelson (2/19/22): Parameterized Vietoris-Rips Filtrations via Covers
A challenge in computational topology is to deal with large filtered geometric complexes built from point cloud data such as Vietoris-Rips filtrations. This has led to the development of schemes for parallel computation and compression which restrict simplices to lie in open sets in a cove
From playlist Vietoris-Rips Seminar

ITHT: Part 12- Model Structure on Topological Spaces
Credits: nLab: https://ncatlab.org/nlab/show/Introduction+to+Homotopy+Theory#TheClassicalModelStructureOfTopologicalSpaces Animation library: https://github.com/3b1b/manim My own code/modified library: https://github.com/treemcgee42/youtub...
From playlist Introduction to Homotopy Theory

Stable Homotopy Seminar, 7: Constructing Model Categories
A stroll through the recognition theorem for cofibrantly generated model categories, using it to construct (1) the Quillen/Serre model structure on topological spaces and (2) the levelwise model structure on spectra. The latter captures the idea that spectra are sequences of spaces, but no
From playlist Stable Homotopy Seminar

Introduction to Homotopy Theory: Part 8- Homotopy in Model Categories
Credits: nLab: https://ncatlab.org/nlab/show/Introduction+to+Homotopy+Theory#homotopy_2 Animation library: https://github.com/3b1b/manim My own code/modified library: https://github.com/treemcgee42/youtube Music: ► Artist Attribution • Music By: "KaizanBlu" • Track Name: "Remembe
From playlist Introduction to Homotopy Theory

What's a Directed Acyclic Graph (DAG)?
The first 40 minutes here introduce the necessary graph theory. Me on the blockchain data structure: https://youtu.be/w3sI8WVX-cc The mentioned article on IOTA: http://elm.nyc/research-1/2018/2/15/iota-tangle-eli5 Jackson Palmer on 3 projects using DAGs: https://youtu.be/LtWUJtnQbKs Conste
From playlist Programming

This video is about metric spaces and some of their basic properties.
From playlist Basics: Topology

Due to the COVID-19 pandemic, Carnegie Mellon University is protecting the health and safety of its community by holding all large classes online. People from outside Carnegie Mellon University are welcome to tune in to see how the class is taught, but unfortunately Prof. Loh will not be o
From playlist CMU 21-228 Discrete Mathematics

Introduction to Homotopy Theory- Part 4: Fibrations
Wow! This one was a lot more detailed than usual, so I'd really recommend going through the proofs with the nLab in hand. I tried to elucidate some of their explanations, but it's still good to have both, so hopefully in between both of our presentations you can find understanding. And as
From playlist Introduction to Homotopy Theory
This lecture is on Introduction to Higher Mathematics (Proofs). For more see http://calculus123.com.
From playlist Proofs

ITHT: Part 11- Quillen Adjunctions
Credits: nLab: https://ncatlab.org/nlab/show/Introduction+to+Homotopy+Theory#QuillenAdjunctions Animation library: https://github.com/3b1b/manim My own code/modified library: https://github.com/treemcgee42/youtub... Music: ► Artist Attribution • Music By: "KaizanBlu" • Track Na
From playlist Introduction to Homotopy Theory