
Subsequence Definition In this video, I define the notion of a subsequence and illustrate with some examples. I also show that if a sequence converges, then any subsequence converges as well Check out my Sequences Playlist: https://www.youtube.com/watch?v=collx3am6II&list=PLJb1qAQIrmmCu
From playlist Sequences

Intro to Subsequences | Real Analysis
What are subsequences in real analysis? In today's lesson we'll define subsequences, and see examples and nonexamples of subsequences. We can learn a lot about a sequence by studying its subsequence, so let's talk about it! If (a_n) is a sequence, we can denote a subsequence of (a_n) as (
From playlist Real Analysis

Math 131 Fall 2018 102918 Subsequences
Definition of subsequence. A sequence converges iff every subsequence converges. Sequence in a compact space has a convergent subsequence. Corollary: bounded sequences in Euclidean space have convergent subsequences. Cauchy sequences. Convergent implies Cauchy. Definition of diameter
From playlist Course 7: (Rudin's) Principles of Mathematical Analysis (Fall 2018)

An Important Fact about Subsequences | Real Analysis
The kth term of a subsequence is at least k terms into the original sequence. We talk about this ad nauseam in today's real analysis video lesson. If we say (a_n) is a sequence and (a_{n_k}) is a subsequence, then we can say n_k is greater than or equal to k. This is what we will be discus
From playlist Real Analysis

An introduction to subtraction, the terms and concepts involved, and subtraction as the opposite of addition. Some example problems are carefully worked and explained. From the Prealgebra course by Derek Owens. This course is available online at http://www.LucidEducation.com.
From playlist Prealgebra Chapter 1 (Complete chapter)

Ex 2: Subtracting Signed Fractions
This video provides two examples of subtracting signed fractions. Complete Video Library at http://www.mathispower4u.com
From playlist Adding and Subtracting Fractions

What is an Injective Function? Definition and Explanation
An explanation to help understand what it means for a function to be injective, also known as one-to-one. The definition of an injection leads us to some important properties of injective functions! Subscribe to see more new math videos! Music: OcularNebula - The Lopez
From playlist Functions

01b Spatial Data Analytics: Subsurface Data
Lecture of the data available for subsurface modeling.
From playlist Spatial Data Analytics and Modeling

Math 101 Introduction to Analysis 110215: Subsequences
Subsequences: definition of; observation about subsequences of convergent sequences; consequences. Subsequential limits. Definition of lim sup, lim inf using subsequential limits. Sketch of proof of Bolzano-Weierstrass theorem for sequences.
From playlist Course 6: Introduction to Analysis

Prove Sequence Diverges with Subsequences | Real Analysis
We can use subsequences to prove a sequence diverges! We'll go over how and why in today's real analysis video lesson. This all comes from the subsequence limit theorem we proved, stating that a sequence converges to L if and only if every subsequence converges to L. Then the idea is as fo
From playlist Real Analysis

Proof: Monotone Sequence has Monotone Subsequences | Real Analysis
We prove if a sequence is monotone then all of its subsequences are monotone. In particular, we prove that all subsequences of an increasing sequence are increasing and all subsequences of a decreasing sequence are decreasing. We prove this using the definition of a monotone sequence. #Rea
From playlist Real Analysis

Sequence Converges iff Every Subsequences Converge to the Same Limit | Real Analysis
A sequence converges to a limit L if and only if every subsequence converges to L. We prove this wonderful result about subsequences in real analysis in today's video lesson! First we prove that if a sequence converges to a limit, then all of its subsequences converge to that same limit. T
From playlist Real Analysis

Monotone Subsequence Theorem (Every Sequence has Monotone Subsequence) | Real Analysis
How nice of a subsequence does any given sequence has? We've seen that not every sequence converges, and some don't even have convergent subsequences. But today we'll prove what is sometimes called the Monotone Subsequence theorem, telling us that every sequence has a monotone subsequence.
From playlist Real Analysis

Sequence (1^n) Diverges using Subsequences | Real Analysis
We prove the sequence (-1)^n diverges by finding two subsequences of (-1)^n that converge to different limits. We previously proved (-1)^n diverges by using a contradiction argument, assuming it does converge to some real number L and showing an absurdity. However, now that we have proven
From playlist Real Analysis

Modern Time Series Analysis with STUMPY || Sean Law
Traditional time series analysis techniques have found success in a variety of data mining tasks. However, they often require years of experience to master and the recent development of straightforward, easy-to-use analysis tools has been lacking. STUMPY is a scientific Python library for
From playlist Python

If Sequence Diverges to Infinity then so do Subsequences | Real Analysis
A sequence diverges to infinity if and only if all of its subequences diverge to infinity. We prove this nice result about divergent sequences and divergent subsequences in today's real analysis video lesson by the river! #RealAnalysis #MathOutside The proof proceeds simply with the defin
From playlist Real Analysis
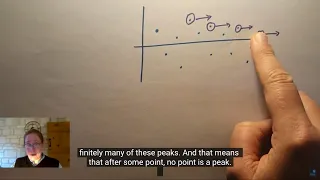
Analysis 1 - Convergent Subsequences: Oxford Mathematics 1st Year Student Lecture
This is the third lecture we're making available from Vicky Neale's Analysis 1 course for First Year Oxford Mathematics Students. Vicky writes: Does every sequence have a convergent subsequence? Definitely no, for example 1, 2, 3, 4, 5, 6, ... has no convergent subsequence. Does every b
From playlist Oxford Mathematics 1st Year Student Lectures

Short Proof of Bolzano-Weierstrass Theorem for Sequences | Real Analysis
Every bounded sequence has a convergent subsequence. This is the Bolzano-Weierstrass theorem for sequences, and we prove it in today's real analysis video lesson. We'll use two previous results that make this proof short and easy. First is the monotone subsequence theorem, stating that eve
From playlist Real Analysis
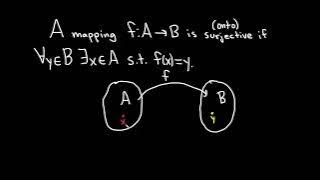
Definition of a Surjective Function and a Function that is NOT Surjective
We define what it means for a function to be surjective and explain the intuition behind the definition. We then do an example where we show a function is not surjective. Surjective functions are also called onto functions. Useful Math Supplies https://amzn.to/3Y5TGcv My Recording Gear ht
From playlist Injective, Surjective, and Bijective Functions