
Teach Astronomy - The Shape of Space
http://www.teachastronomy.com/ According to the theory of general relativity, the universe and the space we live in may actually have a shape, and the shape need not be the flat infinite space described by Euclidean geometry. Infinite space will be flat, but curved space could be finite o
From playlist 22. The Big Bang, Inflation, and General Cosmology
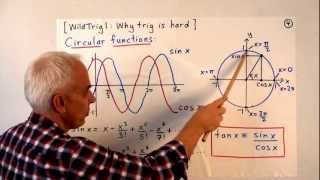
Classical spherical trigonometry | Universal Hyperbolic Geometry 36 | NJ Wildberger
This video presents a summary of classical spherical trigonometry. First we define spherical distance between two points on a sphere, then the angle between two lines on a sphere (i.e. great circles). After a quick reminder of the circular functions cos,sin and tan, we present the main la
From playlist Universal Hyperbolic Geometry

Spherical Volume (2 of 2: Derivation of the Volume of a Sphere through Solids of Revolution)
More resources available at www.misterwootube.com
From playlist Applications of Calculus

Definition of spherical coordinates | Lecture 33 | Vector Calculus for Engineers
We define the relationship between Cartesian coordinates and spherical coordinates; the position vector in spherical coordinates; the volume element in spherical coordinates; the unit vectors; and how to differentiate the spherical coordinate unit vectors. Join me on Coursera: https://www
From playlist Vector Calculus for Engineers

What is the shape of the universe?
Subscribe to our YouTube Channel for all the latest from World Science U. Visit our Website: http://www.worldscienceu.com/ Like us on Facebook: https://www.facebook.com/worldscienceu Follow us on Twitter: https://twitter.com/worldscienceu
From playlist Science Unplugged: Cosmology
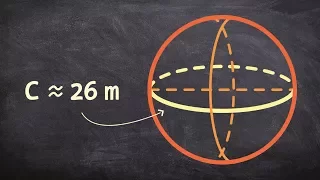
Find the volume of a sphere given the circumference
👉 Learn how to find the volume and the surface area of a sphere. A sphere is a perfectly round 3-dimensional object. It is an object with the shape of a round ball. The distance from the center of a sphere to any point on its surface is called the radius of the sphere. A sphere has a unifo
From playlist Volume and Surface Area

The video explains how to determine the center and radius of a sphere. http://mathispower4u.yolasite.com/
From playlist Vectors

Have you ever noticed that everything in space is a sphere? The Sun, the Earth, the Moon and the other planets and their moons... all spheres. Except for the stuff which isn't spheres. What's going on?
From playlist Guide to Space

Introduction to Spherical Coordinates
Introduction to Spherical Coordinates This is a full introduction to the spherical coordinate system. The definition is given and then the formulas for converting rectangular to spherical and spherical to rectangular. We also look at some of the key graphs in spherical coordinates. Final
From playlist Calculus 3

Talk by Jonathan Wang (MIT, USA)
L-functions and Geometric Harmonic Analysis on Spherical Varieties
From playlist Seminars: Representation Theory and Number Theory

17/11/2015 - Mihalis Dafermos - The stability problem for black holes...
The stability problem for black holes & the cosmic censorship conjectures https://philippelefloch.files.wordpress.com/2015/11/2015-ihp-mihalisdafermos.pdf
From playlist 2015-T3 - Mathematical general relativity - CEB Trimester

IGA: Luca di Cerbo - The Singer conjecture in dimension three revisited and its extensions
Abstract: In this talk, I will show how Price inequalities for harmonic forms combined with some standard topology and geometry of 3-manifolds imply the Singer conjecture in dimension three. This provides an alternative proof of a result of Lott and Lueck (Invent. Math., 1995). Finally, I
From playlist Informal Geometric Analysis Seminar

R. Bamler - Uniqueness of Weak Solutions to the Ricci Flow and Topological Applications 1
I will present recent work with Kleiner in which we verify two topological conjectures using Ricci flow. First, we classify the homotopy type of every 3-dimensional spherical space form. This proves the Generalized Smale Conjecture and gives an alternative proof of the Smale Conjecture, wh
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

Michael Farber: Topology of large random spaces
The lecture was held within the framework of the Hausdorff Trimester Program : Applied and Computational Algebraic Topology I will discuss various models producing large random spaces (simplicial complexes and closed manifolds). The main goal is to analyse properties which hold with proba
From playlist HIM Lectures: Special Program "Applied and Computational Algebraic Topology"

Christoph Winges: Automorphisms of manifolds and the Farrell Jones conjectures
The lecture was held within the framework of the Hausdorff Trimester Program: K-Theory and Related Fields. Building on previous work of Bartels, Lück, Reich and others studying the algebraic K-theory and L-theory of discrete group rings, the validity of the Farrell-Jones Conjecture has be
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"

Dynamical systems on homogenous spaces and number theory by Anish Ghosh
Geometry, Groups and Dynamics (GGD) - 2017 DATE: 06 November 2017 to 24 November 2017 VENUE: Ramanujan Lecture Hall, ICTS, Bengaluru The program focuses on geometry, dynamical systems and group actions. Topics are chosen to cover the modern aspects of these areas in which research has b
From playlist Geometry, Groups and Dynamics (GGD) - 2017

R. Bamler - Uniqueness of Weak Solutions to the Ricci Flow and Topological Applications 1 (vt)
I will present recent work with Kleiner in which we verify two topological conjectures using Ricci flow. First, we classify the homotopy type of every 3-dimensional spherical space form. This proves the Generalized Smale Conjecture and gives an alternative proof of the Smale Conjecture, wh
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

Bruce KLEINER - Ricci flow, diffeomorphism groups, and the Generalized Smale Conjecture
The Smale Conjecture (1961) may be stated in any of the following equivalent forms: • The space of embedded 2-spheres in R3 is contractible. • The inclusion of the orthogonal group O(4) into the group of diffeomorphisms of the 3-sphere is a homotopy equivalence. • The s
From playlist Riemannian Geometry Past, Present and Future: an homage to Marcel Berger

C. Li - Classifying sufficiently connected PSC manifolds in 4 and 5 dimensions
In this talk, I will discuss some recent developments on the topology of closed manifolds admitting Riemannian metrics of positive scalar curvature. In particular, we will prove if a closed PSC manifold of dimension 4 (resp. 5) has vanishing π2 (resp. vanishing π2 and π3), then a finite co
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

(January 28, 2013) Leonard Susskind presents three possible geometries of homogeneous space: flat, spherical, and hyperbolic, and develops the metric for these spatial geometries in spherical coordinates. Originally presented in the Stanford Continuing Studies Program. Stanford Universit
From playlist Lecture Collection | Cosmology