
In this video I write down the axioms of Lie algebras and then discuss the defining anti-symmetric bilinear map (the Lie bracket) which is zero on the diagonal and fulfills the Jacobi identity. I'm following the compact book "Introduction to Lie Algebras" by Erdmann and Wildon. https://gi
From playlist Algebra

The Lie-algebra of Quaternion algebras and their Lie-subalgebras
In this video we discuss the Lie-algebras of general quaternion algebras over general fields, especially as the Lie-algebra is naturally given for 2x2 representations. The video follows a longer video I previously did on quaternions, but this time I focus on the Lie-algebra operation. I st
From playlist Algebra

Lie groups: Poincare-Birkhoff-Witt theorem
This lecture is part of an online graduate course on Lie groups. We state the Poincare-Birkhoff Witt theorem, which shows that the universal enveloping algebra (UEA) of a Lie algebra is the same size as a polynomial algebra. We prove it for Lie algebras of Lie groups and sketch a proof of
From playlist Lie groups

Pavel Etingof: Poisson-Lie groups and Lie bialgebras - Lecture 1
HYBRID EVENT Recorded during the meeting "Lie Theory and Poisson Geometry" the January 10, 2022 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM's Audiov
From playlist Virtual Conference

Topological interpretations of knots, curves & more
International visitors from Toronto visited SMRI to work on a topological algebra project with University of Sydney mathematician Dr Zsuzsanna Dancso. Professor Dror Bar-Natan (University of Toronto), Dr Nancy Scherich (Elon University) and PhD candidate Jessica Liu (University of Toronto)
From playlist SMRI Interviews

Loïc FOISSY - Cointeracting Bialgebras
Pairs of cointeracting bialgebras recently appears in the literature of combinatorial Hopf algebras, with examples based on formal series, on trees (Calaque, Ebrahimi-Fard, Manchon), graphs (Manchon), posets... We will give several results obtained on pairs of cointeracting bialgebras: act
From playlist Algebraic Structures in Perturbative Quantum Field Theory: a conference in honour of Dirk Kreimer's 60th birthday

This lecture is part of an online graduate course on Lie groups. This lecture is about Lie's theorem, which implies that a complex solvable Lie algebra is isomorphic to a subalgebra of the upper triangular matrices. . For the other lectures in the course see https://www.youtube.com/playl
From playlist Lie groups

Pavel Etingof: Poisson-Lie groups and Lie bialgebras - Lecture 2
HYBRID EVENT Recorded during the meeting "Lie Theory and Poisson Geometry" the January 11, 2022 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM's Audiov
From playlist Virtual Conference

Pavel Etingof: Poisson-Lie groups and Lie bialgebras - Lecture 3
HYBRID EVENT Recorded during the meeting "Lie Theory and Poisson Geometry" the January 12, 2022 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM's Audiov
From playlist Virtual Conference

Yvain BRUNED - Bogoliubov Type Recursions for Renormalisation in Regularity Structures
Hairer's regularity structures transformed the solution theory of singular stochastic partial differential equations. The notions of positive and negative renormalisation are central and the intricate interplay between these two renormalisation procedures is captured through the combinatio
From playlist Algebraic Structures in Perturbative Quantum Field Theory: a conference in honour of Dirk Kreimer's 60th birthday

Gérard H E Duchamp - Kleene Stars in Shuffle Algebras
We present some bialgebras and their monoid of characters. We entend, to the case of some rings, the well-known theorem (in the case when the scalars form a field) about linear independence of characters. Examples of algebraic independence of subfamilies and identites derived from their gr
From playlist Combinatorics and Arithmetic for Physics: 02-03 December 2020

Lie derivatives of differential forms
Introduces the lie derivative, and its action on differential forms. This is applied to symplectic geometry, with proof that the lie derivative of the symplectic form along a Hamiltonian vector field is zero. This is really an application of the wonderfully named "Cartan's magic formula"
From playlist Symplectic geometry and mechanics

The Weyl algebra and the Heisenberg Lie algebra
In this video we give a simple teaser into the world of operator algebras. In particular, we talk about the Weyl algebra and compute some expressions that fulfill the property which defines the Heisenberg Lie algebra http://math.uchicago.edu/~may/REU2012/REUPapers/Lingle.pdf https://en.w
From playlist Algebra

This lecture is part of an online graduate course on Lie groups. We define the Lie algebra of a Lie group in two ways, and show that it satisfied the Jacobi identity. The we calculate the Lie algebras of a few Lie groups. For the other lectures in the course see https://www.youtube.co
From playlist Lie groups

Lie groups: Lie groups and Lie algebras
This lecture is part of an online graduate course on Lie groups. We discuss the relation between Lie groups and Lie algebras, and give several examples showing how they behave differently. Lie algebras turn out to correspond more closely to the simply connected Lie groups. We then explain
From playlist Lie groups
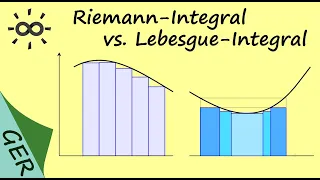
Riemann-Integral vs. Lebesgue-Integral
English version here: https://www.youtube.com/watch?v=PGPZ0P1PJfw Unterstützt den Kanal auf Steady: https://steadyhq.com/en/brightsideofmaths Ihr werdet direkt informiert, wenn ich einen Livestream anbiete. Hier erkläre ich den Unterschied zwischen Riemann-Integral und Lebesgue-Integral
From playlist Analysis

PBS Member Stations rely on viewers like you. To support your local station, go to: http://to.pbs.org/DonateOKAY ↓ More info and sources below ↓ We’re on PATREON! Join the community ►► https://www.patreon.com/itsokaytobesmart SUBSCRIBE so you don’t miss a video! ►► http://bit.ly/iotbs_sub
From playlist Be Smart - LATEST EPISODES!

Probability that a Person did Not Lie During a Polygraph Test
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Probability that a Person did Not Lie During a Polygraph Test
From playlist Statistics

NOTACON 6: The Strange and Creepy World of Brain Fingerprinting
Speaker: Ne0nRa1n Imagine a world in the future where your thoughts could be used against you to sentence you for a crime, could decide if you will be allowed fly on an airplane, or could decided whether or not your own government considers you a terrorist. Sound like something out of dys
From playlist Notacon 6

In this video, I show how to calculate the integral of x^3 from 0 to 1 but using the Lebesgue integral instead of the Riemann integral. My hope is to show you that they indeed produce the same answer, and that in fact Riemann integrable functions are also Lebesgue integrable. Enjoy!
From playlist Real Analysis