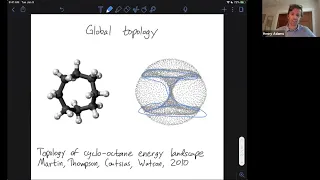
Fractal dimension on networks
Fractal analysis is useful in the study of complex networks, present in both natural and artificial systems such as computer systems, brain and social networks, allowing further development of the field in network science. (Wikipedia).