
Introduction to additive combinatorics lecture 1.8 --- Plünnecke's theorem
In this video I present a proof of Plünnecke's theorem due to George Petridis, which also uses some arguments of Imre Ruzsa. Plünnecke's theorem is a very useful tool in additive combinatorics, which implies that if A is a set of integers such that |A+A| is at most C|A|, then for any pair
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)

Introduction to additive combinatorics lecture 1.0 --- What is additive combinatorics?
This is an introductory video to a 16-hour course on additive combinatorics given as part of Cambridge's Part III mathematics course in the academic year 2021-2. After a few remarks about practicalities, I informally discuss a few open problems, and attempt to explain what additive combina
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)

Jean-Marie de Koninck: On the proximity of additive and multiplicative functions
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Number Theory
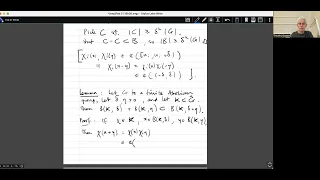
Introduction to additive combinatorics lecture 10.1 --- the structure and properties of Bohr sets.
An important informal idea in additive combinatorics is that of a "structured" set. One example of a class of sets that are rich in additive structure is the class of Bohr sets, which play the role in general finite Abelian groups that subspaces play in the special case of groups of the fo
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)
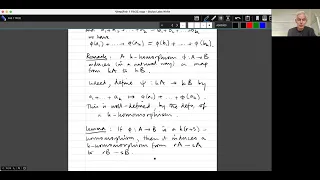
Introduction to additive combinatorics lecture 5.8 --- Freiman homomorphisms and isomorphisms.
The notion of a Freiman homomorphism and the closely related notion of a Freiman isomorphism are fundamental concepts in additive combinatorics. Here I explain what they are and prove a lemma that states that a subset A of F_p^N such that kA - kA is not too large is "k-isomorphic" to a sub
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)

Introduction to additive combinatorics lecture 11.2 --- Part of the proof of Roth's theorem
Roth's theorem, one of the fundamental results of additive combinatorics, states that for every positive δ and every positive integer k there exists a positive integer n such that every subset of {1,2,...,n} of size at least δn contains an arithmetic progression of length 3. (This was late
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)
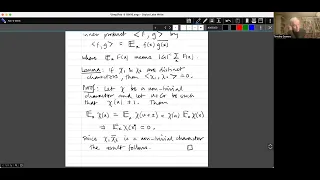
Introduction to additive combinatorics lecture 7.3 -- dual groups and the discrete Fourier transform
The discrete Fourier transform is a fundamental tool in additive combinatorics that makes it possible to prove many interesting results that would be very hard or even impossible to prove otherwise. Here I discuss the characters on a finite Abelian group G, prove that they are orthogonal a
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)

Introduction to additive combinatorics lecture 10.8 --- A weak form of Freiman's theorem
In this short video I explain how the proof of Freiman's theorem for subsets of Z differs from the proof given earlier for subsets of F_p^N. The answer is not very much: the main differences are due to the fact that cyclic groups of prime order do not have lots of subgroups, so one has to
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)

Topics in Combinatorics lecture 13.8 --- The slice rank of a diagonal 3-tensor
A result that has played a central role in additive combinatorics is the statement that for every positive c there exists n such that every subset of F_3^n of density at least c contains three distinct vectors x, y and z such that x + y + z = 0. For a long time, a major open problem was to
From playlist Topics in Combinatorics (Cambridge Part III course)

Yonatan Harpaz - New perspectives in hermitian K-theory III
For questions and discussions of the lecture please go to our discussion forum: https://www.uni-muenster.de/TopologyQA/index.php?qa=k%26l-conference This lecture is part of the event "New perspectives on K- and L-theory", 21-25 September 2020, hosted by Mathematics Münster: https://go.wwu
From playlist New perspectives on K- and L-theory

Yonatan Harpaz - New perspectives in hermitian K-theory II
Warning: around 32:30 in the video, in the slide entitled "Karoubi's conjecture", a small mistake was made - in the third bulleted item the genuine quadratic structure appearing should be the genuine symmetric one (so both the green and red instances of the superscript gq should be gs), an
From playlist New perspectives on K- and L-theory

Recent developments in non-commutative Iwasawa theory I - David Burns
David Burns March 25, 2011 For more videos, visit http://video.ias.edu
From playlist Mathematics

Additive Number Theory: Extremal Problems and the Combinatorics.... (Lecture 1) by M. Nathanson
Program Workshop on Additive Combinatorics ORGANIZERS: S. D. Adhikari and D. S. Ramana DATE: 24 February 2020 to 06 March 2020 VENUE: Madhava Lecture Hall, ICTS Bangalore Additive combinatorics is an active branch of mathematics that interfaces with combinatorics, number theory, ergod
From playlist Workshop on Additive Combinatorics 2020

Ulrich Bunke: Coarse homotopy theory and K-theory
Talke by Ulrich Bundle in Global Noncommutative Geometry Seminar (Americas) on September 30, 2022. https://globalncgseminar.org/talks/tba-36/
From playlist Global Noncommutative Geometry Seminar (Americas)

Charles Weibel: K-theory of algebraic varieties (Lecture 2)
The lecture was held within the framework of the Hausdorff Trimester Program: K-Theory and Related Fields. Charles Weibel: K theory of algebraic varieties Abstract: Lecture 1 will present definitions for the Waldhausen K-theory of rings, varieties, additive and exact categories, and dg c
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"
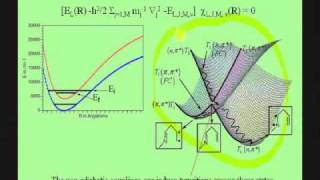
Lecture 01-Jack Simons Electronic Structure Theory- Born-Oppenheimer approximation
The Born-Oppenheimer approximation; non-adiabatic couplings; the electronic and vibration-rotation Schrodigner equations; atomic units; electronic cusps, electronic wave functions and energy surfaces; orbitals and spin-orbitals, Slater determinants; effects of antisymmetry; problems arisin
From playlist U of Utah: Jack Simons' Electronic Structure Theory course

Lars Hesselholt: The big de Rham Witt complex
The lecture was held within the framework of the Hausdorff Trimester Program: Non-commutative Geometry and its Applications and the Workshop: Number theory and non-commutative geometry 26.11.2014
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"

Additive number theory: Extremal problems and the combinatorics of sum. (Lecture 4) by M. Nathanson
Program Workshop on Additive Combinatorics ORGANIZERS: S. D. Adhikari and D. S. Ramana DATE: 24 February 2020 to 06 March 2020 VENUE: Madhava Lecture Hall, ICTS Bangalore Additive combinatorics is an active branch of mathematics that interfaces with combinatorics, number theory, ergod
From playlist Workshop on Additive Combinatorics 2020

P. Scholze - p-adic K-theory of p-adic rings
The original proof of Grothendieck's purity conjecture in étale cohomology (the Thomason-Gabber theorem) relies on results on l-adic K-theory and its relation to étale cohomology when l is invertible. Using recent advances of Clausen-Mathew-Morrow and joint work with Bhatt and Morrow, our
From playlist Arithmetic and Algebraic Geometry: A conference in honor of Ofer Gabber on the occasion of his 60th birthday