
ADVERBS OF DEGREE - ENGLISH GRAMMAR
Adverbs of degree are words that describe or modify adjectives or adverbs. They are a special type of adverb, so I don't really like to think of them as adverbs. They are best on their own category. These are also called intensifiers or qualifiers. If you want to support the channel, hit
From playlist English Grammar

Multiplying Roman Numerals the Ancient Way #shorts
Check out the main channel @polymathematic ! Because the Roman numeral system doesn't rely on place value like our decimal number system, it can be very hard to multiply two numbers together. There are various workarounds you can do with distribution and looking up values in tables, but t
From playlist polymathematic #shorts

Concepts vs Typeclasses vs Traits vs Protocols
C++ Concepts Haskell Typeclasses Rust Traits Swift Protocols EVENT: Meeting C++ 2020 SPEAKER: Conor Hoekstra PUBLICATION PERMISSIONS: The author provided Coding Tech with the permission to republish this video. **** Become a more effective Developer by using Kite! Kite is a free AI-
From playlist Software Development

Why Algebraic Data Types Are Important
Strong static typing detects a lot of bugs at compile time, so why would anyone prefer to program in JavaScript or Python? The main reason is that type systems can be extremely complex, often with byzantine typing rules (C++ comes to mind). This makes generic programming a truly dark art.
From playlist Functional Programming

Programming with Math (Exploring Type Theory)
As programs are getting more complex, it's time to go back to basics, to the old well tested approach to complexity called mathematics. Let compilers deal with the intricacies of Turing machines. Our strength is abstract thinking. Let's use it! EVENT: Øredev 2018 SPEAKER: Bartosz Milew
From playlist Software Development

JavaScript Snake Game Tutorial Using Functional Programming
Build a Snake Game in JavaScript using Functional Programming concepts. No libraries are used in this JavaScript tutorial. 💻 Source code: https://github.com/chrokh/snake Created by Christopher Okhravi. 🔗Check out his YouTube channel: https://www.youtube.com/channel/UCbF-4yQQAWw-UnuCd2Azf
From playlist JavaScript Tutorials

Differential Equations | Convolution: Definition and Examples
We give a definition as well as a few examples of the convolution of two functions. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Differential Equations

Evolutionary Genetics in the Crush of Genomics
Charles H. Langley, UC Davis Simons Institute Open Lectures http://simons.berkeley.edu/events/openlectures2014-spring-3
From playlist Simons Institute Berkeley

2022 PROG2006 Introduction to the course. Core logistics.
From playlist PROG2006 - Programming

Iterators are a generalization of lists that are accessed one element at a time. Iterators allow us to work with data whose length is infinite or unknown, and they avoid the explicit generation of all elements at the same time, by using incremental generators. First presented a year ago, t
From playlist Wolfram Technology Conference 2022

Parametric equations on one Cartesian path (1 of 2: Introduction)
More resources available at www.misterwootube.com
From playlist Mathematical Exploration
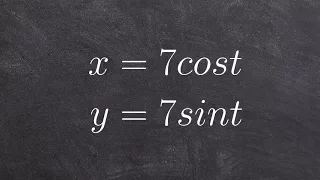
Learn how to eliminate the parameter given sine and cosine of t
Learn how to eliminate the parameter in a parametric equation. A parametric equation is a set of equations that express a set of quantities as explicit functions of a number of independent variables, known as parameters. Eliminating the parameter allows us to write parametric equation in r
From playlist Parametric Equations

Solving an equation with brackets
👉 Learn how to solve multi-step equations. An equation is a statement stating that two values are equal. A multi-step equation is an equation which can be solved by applying multiple steps of operations to get the solution. To solve a multi-step equation, we first use distribution propert
From playlist How to Solve Multi Step Equations with Brackets

Solving an equation with brackets
👉 Learn how to solve multi-step equations. An equation is a statement stating that two values are equal. A multi-step equation is an equation which can be solved by applying multiple steps of operations to get the solution. To solve a multi-step equation, we first use distribution propert
From playlist How to Solve Multi Step Equations with Brackets

Prepositions in Italian: Preposizioni Articolate
What's a preposition? It's a word that describes a relationship between a noun and some other element in the sentence. In English, these are words like to, at, of, or in. How are they used in Italian? Furthermore, how do these combine with articles to become preposizioni articolate? Let's
From playlist Italian

The lecture was held within the framework of the Hausdorff Trimester Program: Periods in Number Theory, Algebraic Geometry and Physics. Abstract: In an important series of papers, Galkin, Golyshev, and Iritani have introduced the concept of Apery constants of Fano varieties, arising from
From playlist Workshop: "Periods and Regulators"

We show the connection between the method of adjoints in optimal control to the implicit function theorem ansatz. We relate the costate or adjoint state variable to Lagrange multipliers.
From playlist There and Back Again: A Tale of Slopes and Expectations (NeurIPS-2020 Tutorial)


