
What are acute, obtuse, right, and straight angles
👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships
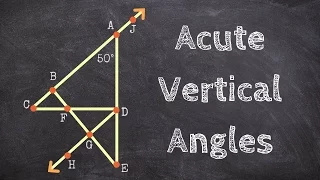
Determining acute vertical angles
👉 Learn how to define and classify different angles based on their characteristics and relationships are given a diagram. The different types of angles that we will discuss will be acute, obtuse, right, adjacent, vertical, supplementary, complementary, and linear pair. The relationships
From playlist Angle Relationships From a Figure

Introduction to Angles (2 of 2: Definition & Basic Details)
More resources available at www.misterwootube.com
From playlist Angle Relationships

CCSS What is the Angle Addition Postulate
👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships

👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships
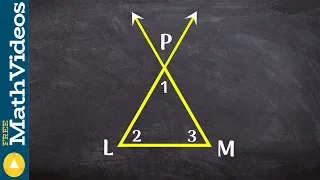
Identify the type of angle from a figure acute, right, obtuse, straight ex 1
👉 Learn how to define and classify different angles based on their characteristics and relationships are given a diagram. The different types of angles that we will discuss will be acute, obtuse, right, adjacent, vertical, supplementary, complementary, and linear pair. The relationships
From playlist Angle Relationships

What is an angle and it's parts
👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships
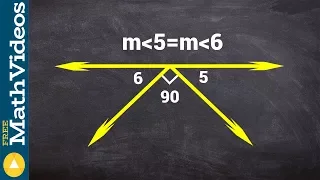
Determine the values of two angles that lie on a lie with a third angle
👉 Learn how to define and classify different angles based on their characteristics and relationships are given a diagram. The different types of angles that we will discuss will be acute, obtuse, right, adjacent, vertical, supplementary, complementary, and linear pair. The relationships
From playlist Angle Relationships From a Figure

Gradient (2 of 3: Angle of inclination)
More resources available at www.misterwootube.com
From playlist Further Linear Relationships

Lecture 4 | Modern Physics: Classical Mechanics (Stanford)
Lecture 4 of Leonard Susskind's Modern Physics course concentrating on Classical Mechanics. Recorded November 5, 2007 at Stanford University. This Stanford Continuing Studies course is the first of a six-quarter sequence of classes exploring the essential theoretical foundations of mod
From playlist Course | Modern Physics: Classical Mechanics

Lecture 7 | Modern Physics: Special Relativity (Stanford)
Lecture 7 of Leonard Susskind's Modern Physics course concentrating on Special Relativity. Recorded May 25, 2008 at Stanford University. This Stanford Continuing Studies course is the first of a six-quarter sequence of classes exploring the essential theoretical foundations of modern ph
From playlist Lecture Collection | Modern Physics: Special Relativity

mod-21 lec-22A Design Analysis of Gear Pumps - I
Fundamentals of Industrial Oil Hydraulics and Pneumatics by Prof. R.N. Maiti,Department of Mechanical Engineering,IIT Kharagpur.For more details on NPTEL visit http://nptel.ac.in
From playlist IIT Kharagpur: Fundamentals of Industrial Oil Hydraulics and Pneumatics (CosmoLearning Mechanical Engineering)

Lecture 7 | String Theory and M-Theory
(November 1, 2010) Leonard Susskind discusses the specifics of strings including Feynman diagrams and mapping particles. String theory (with its close relative, M-theory) is the basis for the most ambitious theories of the physical world. It has profoundly influenced our understanding of
From playlist Lecture Collection | String Theory and M-Theory

Lecture 8 | String Theory and M-Theory
(November 8, 2010) Professor Leonard Susskind covers the history of path/surface integrals; conformal mapping; application of conformal mapping in string scattering. String theory (with its close relative, M-theory) is the basis for the most ambitious theories of the physical world. It ha
From playlist Lecture Collection | String Theory and M-Theory

Alex Wright - Minicourse - Lecture 3
Alex Wright Dynamics, geometry, and the moduli space of Riemann surfaces We will discuss the GL(2,R) action on the Hodge bundle over the moduli space of Riemann surfaces. This is a very friendly action, because it can be explained using the usual action of GL(2,R) on polygons in the plane
From playlist Maryland Analysis and Geometry Atelier

Alex Wright - Minicourse - Lecture 2
Alex Wright Dynamics, geometry, and the moduli space of Riemann surfaces We will discuss the GL(2,R) action on the Hodge bundle over the moduli space of Riemann surfaces. This is a very friendly action, because it can be explained using the usual action of GL(2,R) on polygons in the plane
From playlist Maryland Analysis and Geometry Atelier

Code-It-Yourself! Worms Part #2 (C++)
A nice big project to end the year with! Split into several parts, I show you how to create a game similar to the classic Worms! Written from scratch, in C++ This Video: User Input, Cameras and State Machines Source: https://github.com/OneLoneCoder/Javidx9/tree/master/ConsoleGameEngine/B
From playlist Code-It-Yourself!

October 22, 2012 - Leonard Susskind derives the spacetime metric for a gravitational field, and introduces the relativistic mathematics that describe a black hole. This series is the fourth installment of a six-quarter series that explore the foundations of modern physics. In this quarter
From playlist Lecture Collection | General Relativity
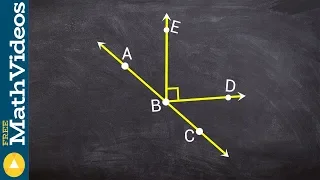
Label the angle in three different ways
👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships

Alex Wright - Minicourse - Lecture 1
Alex Wright Dynamics, geometry, and the moduli space of Riemann surfaces We will discuss the GL(2,R) action on the Hodge bundle over the moduli space of Riemann surfaces. This is a very friendly action, because it can be explained using the usual action of GL(2,R) on polygons in the plane
From playlist Maryland Analysis and Geometry Atelier