
Follow updates on Twitter: https://twitter.com/eigensteve This series discusses exponential growth, which is a ubiquitous phenomenon in science and engineering. This video will provide a high-level overview. Website: https://www.eigensteve.com/
From playlist Intro to Data Science

Abundant, Deficient, and Perfect Numbers ← number theory ← axioms
Integers vary wildly in how "divisible" they are. One way to measure divisibility is to add all the divisors. This leads to 3 categories of whole numbers: abundant, deficient, and perfect numbers. We show there are an infinite number of abundant and deficient numbers, and then talk abou
From playlist Number Theory

Prove that there is a prime number between n and n!
A simple number theory proof problem regarding prime number distribution: Prove that there is a prime number between n and n! Please Like, Share and Subscribe!
From playlist Elementary Number Theory

What’s the biggest number you can think of? Well, what about one more than that number? We can’t really comprehend the idea of infinity, but it’s still a useful concept in science. Brian Greene explains more. Subscribe to our YouTube Channel for all the latest from World Science U. Visit
From playlist Science Unplugged: Physics

The Prime Number Theorem, an introduction ← Number Theory
An introduction to the meaning and history of the prime number theorem - a fundamental result from analytic number theory. Narrated by Cissy Jones Artwork by Kim Parkhurst, Katrina de Dios and Olga Reukova Written & Produced by Michael Harrison & Kimberly Hatch Harrison ♦♦♦♦♦♦♦♦♦♦ Ways t
From playlist Number Theory

Here's a re-enactment of the famous paradox known as the "infinite monkey theorem."
From playlist Cosmic Journeys

Prime Numbers and their Mysterious Distribution (Prime Number Theorem)
Primes are the building blocks of math. But just how mysterious are they? Our study of prime numbers dates back to the ancient Greeks who first recognized that certain numbers can't be turned into rectangles, or that they can't be factored into any way. Over the years prime numbers have
From playlist Prime Numbers

19861: A Superabundant Odyssey - #MegaFavNumbers
A tale of superabundant numbers, the Riemann Hypothesis, and a proof by assumption. This video is part of the #MegaFavNumbers collaboration: https://www.youtube.com/playlist?list=PLar4u0v66vIodqt3KSZPsYyuULD5meoAo Special thanks to Dr. Jonathan Clark and Dr. Ben Braun for their roles in
From playlist MegaFavNumbers

S-T. Yau - Existence of complete Kähler-Einstein metric with negative scalar curvature
This is a talk about my works with Damin Wu concerning those manifolds with negative holomorphic sectional curvature. I shall describe our theorem that such manifold must have negative first Chern class.
From playlist Complex analytic and differential geometry - a conference in honor of Jean-Pierre Demailly - 6-9 juin 2017
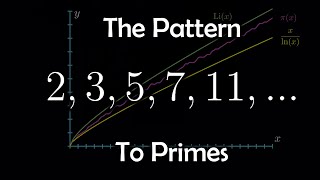
In this video, we explore the "pattern" to prime numbers. I go over the Euler product formula, the prime number theorem and the connection between the Riemann zeta function and primes. Here's a video on a similar topic by Numberphile if you're interested: https://youtu.be/uvMGZb0Suyc The
From playlist Other Math Videos

Mertens Conjecture Disproof and the Riemann Hypothesis | MegaFavNumbers
#MegaFavNumbers The Mertens conjecture is a conjecture is a conjecture about the distribution of the prime numbers. It can be seen as a stronger version of the Riemann hypothesis. It says that the Mertens function is bounded by sqrt(n). The Riemann hypothesis on the other hand only require
From playlist MegaFavNumbers

Jorge Vitório Pereira: Birational transformations preserving codimension one foliations
I will report on a work in progress with Federico Lo Bianco, Erwan Rousseau, and Frédéric Touzet about the structure of codimension one foliations having an infinite group of birational symmetries. Recording during the meeting "Complex Dynamics" the January 27, 2020 at the Centre Internat
From playlist Algebraic and Complex Geometry

On the Fourier coefficients of a Cohen-Eisenstein series by Srilakshmi Krishnamoorthy
12 December 2016 to 22 December 2016 VENUE : Madhava Lecture Hall, ICTS Bangalore The Birch and Swinnerton-Dyer conjecture is a striking example of conjectures in number theory, specifically in arithmetic geometry, that has abundant numerical evidence but not a complete general solution.
From playlist Theoretical and Computational Aspects of the Birch and Swinnerton-Dyer Conjecture

Lecture 6 of Leonard Susskind's Modern Physics concentrating on Cosmology. Recorded March 2, 2009 at Stanford University. This Stanford Continuing Studies course is the fifth of a six-quarter sequence of classes exploring the essential theoretical foundations of modern physics. The topi
From playlist Lecture Collection | Modern Physics: Cosmology

Symplectic convexity? (an ongoing story...)
Joint IAS/Princeton/Montreal/Paris/Tel-Aviv Symplectic Geometry Zoominar Topic: Symplectic convexity? (an ongoing story...) Speaker: Jean Gutt Affiliation: University of Toulouse Date: October 21, 2022 What is the symplectic analogue of being convex? We shall present different ideas to
From playlist Mathematics

Solving Diophantine equations using elliptic curves + Introduction to SAGE by Chandrakant Aribam
12 December 2016 to 22 December 2016 VENUE : Madhava Lecture Hall, ICTS Bangalore The Birch and Swinnerton-Dyer conjecture is a striking example of conjectures in number theory, specifically in arithmetic geometry, that has abundant numerical evidence but not a complete general solution.
From playlist Theoretical and Computational Aspects of the Birch and Swinnerton-Dyer Conjecture

Torsion points of the Jacobian of modular curves X0(p2 ) and non- by Debargha Banerjee
12 December 2016 to 22 December 2016 VENUE : Madhava Lecture Hall, ICTS Bangalore The Birch and Swinnerton-Dyer conjecture is a striking example of conjectures in number theory, specifically in arithmetic geometry, that has abundant numerical evidence but not a complete general solution.
From playlist Theoretical and Computational Aspects of the Birch and Swinnerton-Dyer Conjecture

Visit https://brilliant.org/ThatChemist/ to get started learning STEM for free, and the first 200 people will get 20% off their annual premium subscription. In this video, I discuss the chemistry of skunk spray! This video was sponsored by Brilliant. https://www.patreon.com/thatchemist
From playlist Everyday Chemicals

Comparing the corank of fine Selmer group and Selmer group of elliptic curves by Sudhanshu Shekhar
12 December 2016 to 22 December 2016 VENUE : Madhava Lecture Hall, ICTS Bangalore The Birch and Swinnerton-Dyer conjecture is a striking example of conjectures in number theory, specifically in arithmetic geometry, that has abundant numerical evidence but not a complete general solution.
From playlist Theoretical and Computational Aspects of the Birch and Swinnerton-Dyer Conjecture

Number theory Full Course [A to Z]
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure #mathematics devoted primarily to the study of the integers and integer-valued functions. Number theorists study prime numbers as well as the properties of objects made out of integers (for example, ratio
From playlist Number Theory