
Powered by https://www.numerise.com/ An introduction to basic index notation www.hegartymaths.com http://www.hegartymaths.com/
From playlist Index notation
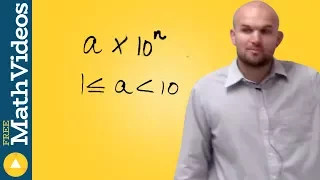
What is the definition of scientific notation
👉 Learn about scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is the number of digits up to t
From playlist Scientific Notation | Learn About

Powered by https://www.numerise.com/ The following video uses the multiplication and division rules for index notation in slightly more complicated cases. www.hegartymaths.com http://www.hegartymaths.com/
From playlist Index notation

The SQL Create Index Statement
This video explains how to use the CREATE INDEX statement of the Structured Query Language (SQL). It is the third in a series about a subset of SQL known as the Data Definition Language (DDL), which can be used to create and modify the table structures within a relational database. It in
From playlist Databases

Determine the product of two very large numbers by converting to scientific notation
👉 Learn how to multiply numbers written in scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is
From playlist Scientific Notation

Raising a scientific number to the third power
👉 Learn how to multiply numbers written in scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is
From playlist Scientific Notation
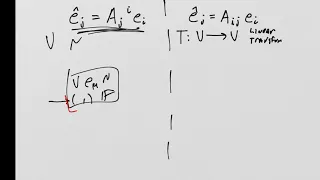
Lie Groups and Lie Algebras: Lesson 8 - the Classical Groups part VI
Lie Groups and Lie Algebras: Lesson 8 - the Classical Groups part VI
From playlist Lie Groups and Lie Algebras

Learn how to determine the product of scientific notation
👉 Learn how to multiply numbers written in scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is
From playlist Scientific Notation

What is General Relativity? Lesson 11: CFREE to COMP conversion
What is General Relativity? Lesson 11: CFREE to COMP conversion
From playlist What is General Relativity?

Finding product of two numbers when they are in scientific notation
👉 Learn how to multiply numbers written in scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is
From playlist Scientific Notation

What is General Relativity? Lesson 46: Symmetries of the Riemann Tensor
What is General Relativity? Lesson 46: Symmetries of the Riemann Tensor Here we review material that shows up so frequently in general relativity mathematics that was simply must push through it and become comfortable with it. Please consider supporting this channel via Patreon: https:/
From playlist What is General Relativity?

Lec 4b - Phys 237: Gravitational Waves with Kip Thorne
Watch the rest of the lectures on http://www.cosmolearning.com/courses/overview-of-gravitational-wave-science-400/ Redistributed with permission. This video is taken from a 2002 Caltech on-line course on "Gravitational Waves", organized and designed by Kip S. Thorne, Mihai Bondarescu and
From playlist Caltech: Gravitational Waves with Kip Thorne - CosmoLearning.com Physics

What is General Relativity? Lesson 15 The covariant derivative of a (p,q)-rank tensor
In this lesson we review all the CFREE algebraic rules and the COMP conversions and then demonstrate the CFREE and COMP formulas for the covariant derivative of an arbitrary tensor.
From playlist What is General Relativity?

xAct: Efficient Tensor Computer Algebra: Live with the R&D team
Presentation begins at 1:43 In this stream, we have xAct: Efficient Tensor Computer Algebra with Wolfram R&D. Follow us on our official social media channels. Twitter: https://twitter.com/WolframResearch/ Facebook: https://www.facebook.com/wolframresearch/ Instagram: https://www.instagra
From playlist Live with the R&D Team

Lecture 2A: Higher-order Procedures
MIT 6.001 Structure and Interpretation of Computer Programs, Spring 2005 Instructor: Harold Abelson, Gerald Jay Sussman, Julie Sussman View the complete course: https://ocw.mit.edu/6-001S05 YouTube Playlist: https://www.youtube.com/playlist?list=PLE18841CABEA24090 Higher-order Procedures
From playlist MIT 6.001 Structure and Interpretation, 1986
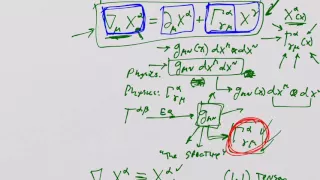
What is a Tensor? Lesson 18: The covariant derivative continued
What is a Tensor? Lesson 18: The covariant derivative continued This lesson covers some of the "coordinate free" language used to describe the covariant derivative. As a whole this lecture is optional. However, becoming comfortable with coordinate free language is probably a good idea. I
From playlist What is a Tensor?

MIT 8.962 General Relativity, Spring 2020 Instructor: Scott Hughes View the complete course: https://ocw.mit.edu/8-962S20 YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP629n_3fX7HmKKgin_rqGzbx More on tensors, derivatives, and 1-forms. Contraction of tensor indices; th
From playlist MIT 8.962 General Relativity, Spring 2020
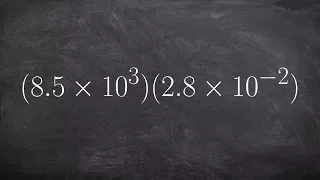
Multiplying numbers in scientific notation
👉 Learn how to multiply numbers written in scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is
From playlist Scientific Notation

Physics 50. Math Methods. Lecture 3.1
UCI Physics 50: Math Methods (Spring 2014). Lec 3.1. Math Methods -- Matrices -- View the complete course: http://ocw.uci.edu/courses/physics_50_math_methods.html Instructor: Micahel Dennin, Ph.D. License: Creative Commons CC-BY-SA Terms of Use: http://ocw.uci.edu/info. More courses at ht
From playlist Physics 50: Math Methods
