
What is the definition of absolute value
http://www.freemathvideos.com In this video playlist you will learn how to solve and graph absolute value equations and inequalities. When working with absolute value equations and functions it is important to understand that the absolute value symbol represents the absolute distance from
From playlist Solve Absolute Value Equations

How To Solve an Absolute Value Equation and Test Our Solutions when They Do Not Work
Learn how to solve absolute value equations with extraneous solutions. Absolute value of a number is the positive value of the number. For instance, the absolute value of 2 is 2 and the absolute value of -2 is also 2. To solve an absolute value problem, we first isolate the absolute value
From playlist Solve Absolute Value Equations
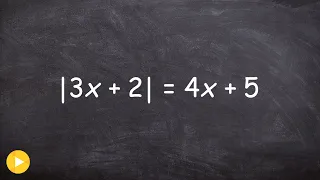
Solving Absolute value equations with a variable on both sides
Learn how to solve absolute value equations with extraneous solutions. Absolute value of a number is the positive value of the number. For instance, the absolute value of 2 is 2 and the absolute value of -2 is also 2. To solve an absolute value problem, we first isolate the absolute value
From playlist Solve Absolute Value Equations

Solving an Absolute Value Equation and Checking for Extraneous Solutions
Learn how to solve absolute value equations with extraneous solutions. Absolute value of a number is the positive value of the number. For instance, the absolute value of 2 is 2 and the absolute value of -2 is also 2. To solve an absolute value problem, we first isolate the absolute value
From playlist Solve Absolute Value Equations

How to evaluate the limit of a function by observing its graph
👉 Learn how to evaluate the limit of an absolute value function. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The absolute value function is a function which only takes the positive val
From playlist Evaluate Limits of Absolute Value

Solving Absolute Value Equations Using Multi Steps
Learn how to solve absolute value equations with extraneous solutions. Absolute value of a number is the positive value of the number. For instance, the absolute value of 2 is 2 and the absolute value of -2 is also 2. To solve an absolute value problem, we first isolate the absolute value
From playlist Solve Absolute Value Equations

Using parent graphs to understand the left and right hand limits
👉 Learn how to evaluate the limit of an absolute value function. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The absolute value function is a function which only takes the positive val
From playlist Evaluate Limits of Absolute Value
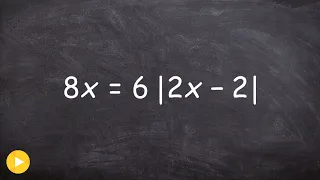
Solving a multi step absolute value equation
Learn how to solve absolute value equations with extraneous solutions. Absolute value of a number is the positive value of the number. For instance, the absolute value of 2 is 2 and the absolute value of -2 is also 2. To solve an absolute value problem, we first isolate the absolute value
From playlist Solve Absolute Value Equations

Evaluate the limit of an absolute value function by direct substitution
👉 Learn how to evaluate the limit of an absolute value function. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The absolute value function is a function which only takes the positive val
From playlist Evaluate Limits of Absolute Value

Rings and modules 4 Unique factorization
This lecture is part of an online course on rings and modules. We discuss unique factorization in rings, showing the implications (Integers) implies (Euclidean domain) implies (Principal ideal domain) implies (Unique factorization domain). We give a few examples to illustrate these implic
From playlist Rings and modules

Imprimitive irreducible representations of finite quasisimple groups by Gerhard Hiss
DATE & TIME 05 November 2016 to 14 November 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore Computational techniques are of great help in dealing with substantial, otherwise intractable examples, possibly leading to further structural insights and the detection of patterns in many abstra
From playlist Group Theory and Computational Methods

Valentin Blomer: The polynomial method for point counting and exponential sums, Lecture 1
We show how families of auxiliary polynomials can be used to count the number of points on certain types of curves over finite fields and to estimate exponential sums and character sums.
From playlist Harmonic Analysis and Analytic Number Theory

Geometry-of-Numbers Techniques in Arithmetic Statistics (Lecture 3) by Arul Shankar
PROGRAM ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (HYBRID) ORGANIZERS: Ashay Burungale (CalTech/UT Austin, USA), Haruzo Hida (UCLA), Somnath Jha (IIT Kanpur) and Ye Tian (MCM, CAS) DATE: 08 August 2022 to 19 August 2022 VENUE: Ramanujan Lecture Hall and online The program pla
From playlist ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (2022)

Introduction to number theory lecture 29. Rings in number theory
This lecture is part of my Berkeley math 115 course "Introduction to number theory" For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj53L8sMbzIhhXSAOpuZ1Fov8 We show how to write several results in number theory, such as the Chines remainder theorem
From playlist Introduction to number theory (Berkeley Math 115)

CTNT 2022 - An Introduction to Galois Representations (Lecture 4) - by Alvaro Lozano-Robledo
This video is part of a mini-course on "An Introduction to Galois Representations" that was taught during CTNT 2022, the Connecticut Summer School and Conference in Number Theory. More about CTNT: https://ctnt-summer.math.uconn.edu/ Note: I was tired after a long event, and may have missp
From playlist CTNT 2022 - An Introduction to Galois Representations (by Alvaro Lozano-Robledo)

On Some Theories of Gauss Sums - Guy Henniart
Geometry and Arithmetic: 61st Birthday of Pierre Deligne Guy Henniart October 17, 2005 Pierre Deligne, Professor Emeritus, School of Mathematics. On the occasion of the sixty-first birthday of Pierre Deligne, the School of Mathematics will be hosting a four-day conference, "Geometry and
From playlist Pierre Deligne 61st Birthday

Calculations with Matrix groups over the integers by Alexander Hulpke
DATE & TIME 05 November 2016 to 14 November 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore Computational techniques are of great help in dealing with substantial, otherwise intractable examples, possibly leading to further structural insights and the detection of patterns in many abstra
From playlist Group Theory and Computational Methods

Calculus 1 lecture - Integrating rational functions
This lecture was re-recorded due to a faulty microphone in the lecture room on 7/10/22. It is part of Calculus 1 (MAST10005) at the University of Melbourne, and covers integrating rational functions using logarithms, arctan and partial fractions. If you're seeing this kind of environment
From playlist Metauni

Valentin Blomer: The polynomial method for point counting and exponential sums, Lecture IV
We show how families of auxiliary polynomials can be used to count the number of points on certain types of curves over finite fields and to estimate exponential sums and character sums.
From playlist Harmonic Analysis and Analytic Number Theory
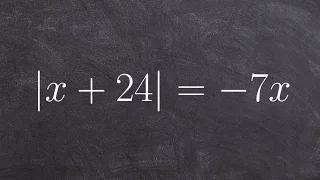
How To Solve an Absolute Value Equation when There is Only One Solution
Learn how to solve absolute value equations with extraneous solutions. Absolute value of a number is the positive value of the number. For instance, the absolute value of 2 is 2 and the absolute value of -2 is also 2. To solve an absolute value problem, we first isolate the absolute value
From playlist Solve Absolute Value Equations