
Jim Bryan : Curve counting on abelian surfaces and threefolds
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebraic and Complex Geometry

Kazuya Kato - Logarithmic abelian varieties
Correction: The affiliation of Lei Fu is Tsinghua University. This is a joint work with T. Kajiwara and C. Nakayama. Logarithmic abelian varieties are degenerate abelian varieties which live in the world of log geometry of Fontaine-Illusie. They have group structures which do not exist in
From playlist Conférence « Géométrie arithmétique en l’honneur de Luc Illusie » - 5 mai 2021

This is one of my all-time favorite differential equation videos!!! :D Here I'm actually using the Wronskian to actually find a nontrivial solution to a second-order differential equation. This is amazing because it brings the concept of the Wronskian back to life! And as they say, you won
From playlist Differential equations

We give a buttload of definitions for morphisms on various categories of complexes. The derived category of an abelian category is a category whose objects are cochain complexes and whose morphisms I describe in this video.
From playlist Derived Categories

Representation theory: Abelian groups
This lecture discusses the complex representations of finite abelian groups. We show that any group is iomorphic to its dual (the group of 1-dimensional representations, and isomorphic to its double dual in a canonical way (Pontryagin duality). We check the orthogonality relations for the
From playlist Representation theory

Claire Voisin: Gonality and zero-cycles of abelian varieties
Abstract: The gonality of a variety is defined as the minimal gonality of curve sitting in the variety. We prove that the gonality of a very general abelian variety of dimension g goes to infinity with g. We use for this a (straightforward) generalization of a method due to Pirola that we
From playlist Algebraic and Complex Geometry

David Masser: Avoiding Jacobians
Abstract: It is classical that, for example, there is a simple abelian variety of dimension 4 which is not the jacobian of any curve of genus 4, and it is not hard to see that there is one defined over the field of all algebraic numbers \overline{\bf Q}. In 2012 Chai and Oort asked if ther
From playlist Algebraic and Complex Geometry
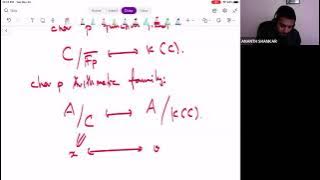
Ananth Shankar, Picard ranks of K3 surfaces and the Hecke orbit conjecture
VaNTAGe Seminar, November 23, 2021
From playlist Complex multiplication and reduction of curves and abelian varieties

RT7.2. Finite Abelian Groups: Fourier Analysis
Representation Theory: With orthogonality of characters, we have an orthonormal basis of L^2(G). We note the basic philosophy behind the Fourier transform and apply it to the character basis. From this comes the definition of convolution, explored in 7.3. Course materials, including pro
From playlist Representation Theory

Complex surfaces 5: Kodaira dimension 0
This talk is an informal survey of the complex projective surfaces of Kodaira number 0. We first explain why there are 4 types of such surfaces (Enriques, K3, hyperelliptic, and abelian) and then give a few examples of each type.
From playlist Algebraic geometry: extra topics

Edgar Costa, From counting points to rational curves on K3 surfaces
VaNTAGe Seminar, Jan 26, 2021
From playlist Arithmetic of K3 Surfaces

Francesc Fité, Sato-Tate groups of abelian varieties of dimension up to 3
VaNTAGe seminar on April 7, 2020 License: CC-BY-NC-SA Closed captions provided by Jun Bo Lau.
From playlist The Sato-Tate conjecture for abelian varieties

Alessandra Sarti, Old and new on the symmetry groups of K3 surfaces
VaNTAGe Seminar, Feb 9, 2021
From playlist Arithmetic of K3 Surfaces

The Geometric Langlands conjecture and non-abelian Hodge theory (Lecture 1) by Ron Donagi
Program: Quantum Fields, Geometry and Representation Theory ORGANIZERS : Aswin Balasubramanian, Saurav Bhaumik, Indranil Biswas, Abhijit Gadde, Rajesh Gopakumar and Mahan Mj DATE & TIME : 16 July 2018 to 27 July 2018 VENUE : Madhava Lecture Hall, ICTS, Bangalore The power of symmetries
From playlist Quantum Fields, Geometry and Representation Theory

Nick Addington - Rational points and derived equivalence - WAGON
For smooth projective varieties over Q, is the existence of a rational point preserved under derived equivalence? First I'll discuss why this question is interesting, and what is known. Then I'll show that the answer is no, giving two counterexamples: an abelian variety and a torsor over i
From playlist WAGON

Jacob explains the fundamental concepts in group theory of what groups and subgroups are, and highlights a few examples of groups you may already know. Abelian groups are named in honor of Niels Henrik Abel (https://en.wikipedia.org/wiki/Niels_Henrik_Abel), who pioneered the subject of
From playlist Basics: Group Theory

Theorem 1.10 - part 09 - Torsion Points of Abelian Varieties
We review some basic galois theory about torsion points of abelian varieties. In the next video we discuss the Serre-Tate theory (not about deformations but about conductors.
From playlist Theorem 1.10
On descending cohomology geometrically - Sebastian Casalaina-Martin
Sebastian Casalaina-Martin University of Colorado at Boulder January 20, 2015 In this talk I will present some joint work with Jeff Achter concerning the problem of determining when the cohomology of a smooth projective variety over the rational numbers can be modeled by an abelian variet
From playlist Mathematics
