
Differential Equations | Abel's Theorem
We present Abel's Theorem with a proof. http://www.michael-penn.net
From playlist Differential Equations

Yuri Tschinkel, Height zeta functions
VaNTAGe seminar May 11, 2021 License: CC-BY-NC-SA
From playlist Manin conjectures and rational points

Theorem 1.10 - part 09 - Torsion Points of Abelian Varieties
We review some basic galois theory about torsion points of abelian varieties. In the next video we discuss the Serre-Tate theory (not about deformations but about conductors.
From playlist Theorem 1.10

Ila Varma, Counting quartic number fields and predicting asymptotics
VaNTAGe Seminar, June 14, 2022 License: CC-BY-NC-SA Links to some of the papers mentioned in this talk: Davenport-Heilbronn I: https://doi.org/10.1112/blms/1.3.345 Davenport-Heilbronn II: http://www.math.toronto.edu/~ila/DH2.pdf Wright: https://doi.org/10.1112/plms/s3-58.1.17 Baily: http
From playlist Arithmetic Statistics II

Every Group of Order Five or Smaller is Abelian Proof
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Every Group of Order Five or Smaller is Abelian Proof. In this video we prove that if G is a group whose order is five or smaller, then G must be abelian.
From playlist Abstract Algebra

Now that we know what quotient groups, a kernel, and normal subgroups are, we can look at the first isomorphism theorem. It states that the quotient group created by the kernel of a homomorphism is isomorphic to the (second) group in the homomorphism.
From playlist Abstract algebra

Introduction to number theory lecture 47. The prime number theorem
This lecture is part of my Berkeley math 115 course "Introduction to number theory" For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj53L8sMbzIhhXSAOpuZ1Fov8 We give an overview of the prime number theorem, stating that the number of primes less tha
From playlist Introduction to number theory (Berkeley Math 115)

Math 139 Fourier Analysis Lecture 32: Fourier Analysis on Finite Abelian Groups
Proving that the dual group has the same order as the group (to show the characters form an orthonormal basis for the functions on the group). Fourier analysis on finite abelian groups: Fourier coefficients; Fourier series; Fourier inversion formula; Plancherel/Parseval theorem. Statemen
From playlist Course 8: Fourier Analysis

Jacob explains the fundamental concepts in group theory of what groups and subgroups are, and highlights a few examples of groups you may already know. Abelian groups are named in honor of Niels Henrik Abel (https://en.wikipedia.org/wiki/Niels_Henrik_Abel), who pioneered the subject of
From playlist Basics: Group Theory

If G is Isomorphic to H then G is Abelian iff H is Abelian Proof
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys If G is Isomorphic to H then G is Abelian iff H is Abelian Proof. This video proves that if there is an isomorphism from a group G to a group H, then G is an abelian group if and only if H is an abelian group.
From playlist Abstract Algebra

Abstract Algebra - 11.1 Fundamental Theorem of Finite Abelian Groups
We complete our study of Abstract Algebra in the topic of groups by studying the Fundamental Theorem of Finite Abelian Groups. This tells us that every finite abelian group is a direct product of cyclic groups of prime-power order. Video Chapters: Intro 0:00 Before the Fundamental Theorem
From playlist Abstract Algebra - Entire Course

High-Energy Conformal Bootstrap and Tauberian Theory - Baurzhan Mukhametzhanov
More videos on http://video.ias.edu
From playlist Natural Sciences

The Fundamental Theorem of Calculus | Algebraic Calculus One | Wild Egg
In this video we lay out the Fundamental Theorem of Calculus --from the point of view of the Algebraic Calculus. This key result, presented here for the very first time (!), shows how to generalize the Fundamental Formula of the Calculus which we presented a few videos ago, incorporating t
From playlist Algebraic Calculus One

Visual Group Theory, Lecture 4.5: The isomorphism theorems
Visual Group Theory, Lecture 4.5: The isomorphism theorems There are four central results in group theory that are collectively known at the isomorphism theorems. We introduced the first of these a few lectures back, under the name of the "fundamental homomorphism theorem." In this lectur
From playlist Visual Group Theory

Andrew Wiles: Fermat's Last theorem: abelian and non-abelian approaches
The successful approach to solving Fermat's problem reflects a move in number theory from abelian to non-abelian arithmetic. This lecture was held by Abel Laurate Sir Andrew Wiles at The University of Oslo, May 25, 2016 and was part of the Abel Prize Lectures in connection with the Abel P
From playlist Sir Andrew J. Wiles

Visual Group Theory, Lecture 4.4: Finitely generated abelian groups
Visual Group Theory, Lecture 4.4: Finitely generated abelian groups We begin this lecture by proving that the cyclic group of order n*m is isomorphic to the direct product of cyclic groups of order n and m if and only if gcd(n,m)=1. Then, we classify all finite abelian groups by decomposi
From playlist Visual Group Theory
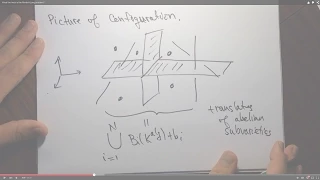
What is the Mordell-Lang problem?
It is my intention to eventually explain some things about the Mordell-Lang problem and the higher dimensional versions of these. The presentation in this video is due to Mazur and can be found in an MSRI article he wrote that introduces these things.
From playlist Mordell-Lang
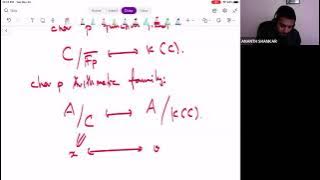
Ananth Shankar, Picard ranks of K3 surfaces and the Hecke orbit conjecture
VaNTAGe Seminar, November 23, 2021
From playlist Complex multiplication and reduction of curves and abelian varieties

On the BSD conjecture for certain families of abelian varieties with ration...- Emmanuel Lecouturier
Joint IAS/Princeton University Number Theory Seminar Topic: On the BSD conjecture for certain families of abelian varieties with rational torsion. Speaker: Emmanuel Lecouturier Affiliation: Member, School of Mathematics Date: March 24, 2022 Let N and p greater than or equal to 5 be prime
From playlist Mathematics

The Structure of the Group of Rational Points of an Abelian Variety (CTNT Online, June 12-14, 2020)
This video was created for the CTNT 2020 Conference (June 12-14, 2020): https://ctnt-summer.math.uconn.edu/ctnt-conference-2020-online/ (Preprint) The Structure of the Group of Rational Points of an Abelian Variety over a Finite Field: https://arxiv.org/abs/2006.00637 My contact informat
From playlist CTNT 2020 - Conference Videos